Probability
Probability Problems
Concepts
Probability: a numerical description of how likely an eventis to occur or how likely it is that a proposition is true.
Combination: A combination is a selection of objects where order is not important.
Permutation: A permutation is an arrangement of objects in a definite order.
Problems
1. In how many different ways can a true-false test consisting of 10 questions be answered?
Each question can be answered 2 different ways, and the answer for one question has no effect on the answer for another (they are independent events).
So, the number of different ways that 10 questions can be answered is :
Answer : 2^10 = 1024
2. A California study concluded that following 7 simple health rules can extend a man’s life by 11 years on the average and a womans life by 7 years. These 7 rules are as follows: no smoking, get regular exercise, use alcohol only in moderation, get 7 to 8 hours of sleep, maintain proper weight, eat breakfast, and do not eat between meals. In how many ways can a person adopt 5 of these rules to follow
(a) if the person presently violates all 7 rules?
7C3
=7!/((7-5)!5!)
=5050/(2*120)
=21
Answer : 21
(b) if the person never drinks and always eats breakfast?
The person never drinks and eat breakfast. So he has already adopted two rules. Now he has to adopt 3 more rules. He has 7-
5C3
=5!/((5-3)!3!)
=120/12
=10
Answer : 21
3. (a) How many three-digit numbers can be formed from the digits 0, 1, 2, 3, 4, 5, and 6 if each digit can be used only once?
6*6*5=180
Answer : 180 ways
(b) How many of these are odd numbers?
3*5*5=75
Answer : 75 ways
(c) How many are greater than 330?
1*3*5=15
3*6*5=90
15+90=105
Answer : 105
4. A pair of fair dice is tossed. Find the probability of getting
(a) a total of 10

Answer : 0.139
(b) at most a total of 4

Answer : 0.278
5. A random sample of 200 adults are classified below by gender and their level of education attained.
| Education | Male | Female |
| Elementary | 38 | 45 |
| Secondary | 28 | 50 |
| College | 22 | 17 |
If a person is picked at random from this group, find the probability that
(a) the person is a male, given that the person has a secondary education;

Answer : 14/39
(b) the person does not have a college degree, given that the person is a female.

Answer : 95/112
6. The probability that a married man watches a certain television show is 0.4, and the probability that a married woman watches the show is 0.5. The probability that a man watches the show, given that his wife does, is 0.7. Find the probability that
(a) a married couple watches the show;

Answer : 0.35
(b) a wife watches the show, given that her husband does;

Answer : 0.875
(c) at least one member of a married couple will watch the show.

Answer : 0.55
7. TheprobabilitythatavehicleenteringtheLurayCavernshasCanadianlicenseplatesis0.12;theprobabilitythatitis a camper is 0.28; and the probability that it is a camper with Canadian license plates is 0.09. What is the probability that
(a) a camper entering the Luray Caverns has Canadian license plates?

Answer : 0.32
(b) a vehicle with Canadian license plates entering the Luray Caverns is a camper?

Answer : 0.75
(c) a vehicle entering the Luray Caverns does not have Canadian plates or is not a camper?

Answer : 0.91
8. Police plan to enforce speed limits by using radar traps at four different locations within the city limits. The radar traps at each of the locations L1, L2, L3, and L4 will be operated 40%, 30%, 20%, and 30% of the time. If a person who is speeding on her way to work has probabilities of 0.2, 0.1, 0.5, and 0.2, respectively, of passing through these locations, what is the probability that she will receive a speeding ticket?
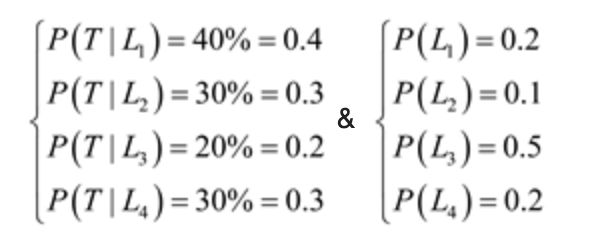

Answer : 0.27
9. A paint-store chain produces and sells latex and semigloss paint. Based on long-range sales, the probability that a customer will purchase latex paint is 0.75. Of those that purchase latex paint, 60% also purchase rollers. But only 30% of semigloss paint buyers purchase rollers. A randomly selected buyer purchases a roller and a can of paint. What is the probability that the paint is latex?

Answer : 0.857
'Studies & Courses > Data Analytics & Stats' 카테고리의 다른 글
| [Probability & Statistics] 4. Bayes’ Rule, Concept of a Random Variable (2) | 2020.04.18 |
|---|---|
| [Probability & Statistics] 2. Sample Space, Events, Counting Sample Points (0) | 2020.04.18 |
| [Probability] Intro to Statistics and Data Analysis (0) | 2020.04.18 |
| [Probability] Probability - Part 2 (0) | 2020.04.05 |
| [Probability] Probability - Part 1 (0) | 2020.04.01 |




댓글