*본 포스팅은 중학교 때 수학을 놓아버린 수포자가 기계학습을 이해하기 위해 정리한 것이므로 정확한 정보가 아닐 수 있습니다. 잘못된 정보는 댓글로 알려주시면 감사하겠습니다.
신경망 구축 과제와 CNN과제를 하면서 Cross Entropy가 딥러닝의 기초 개념이라고하여 찾아보니 Cross Entropy와 KL-divergence는 한 세트로 배우는 것 같아 이번 기회에 정리하고 넘어가보고자 합니다.
Entropy
Entropy는 정보를 표현하는데 필요한 최소 평균 자원량입니다.
"What is a common currency of information?"
여기서 '정보를 표현한다'라는 의미를 이해하기 위해서 언어를 비유할 수 있습니다. 한국어, 일본어, 중국어 등 다양한 언어가 있는데 이를 '만국공통어처럼 사용할 수 있는 언어는 없을까?'와 같은 물음에 Claude Shannon는 Bits이라고 답했습니다. 그래서 여기에서의 '최소 평균 자원량'은 bits로 표현된(0 또는 1로 표현된) 최소 평균 길이라고 말할 수 있습니다.
혁펜하임 님의 강의에서 연인들의 카톡을 예를 들어 설명한 것이 조금 욕이 들어가 있지만 기억이 잘 남는 것 같습니다.
연인의 카톡 내용의 내용을 봤을 때 ❤️를 사용할 확률은 높지만 🖕을 사용할 확률은 적곘죠. 그래서 ❤️를 사용할 확률은 0.5이며 🖕를 0.001이라고 가정한 뒤, 두 가지 케이스를 살펴봅시다.

(Case1) 🖕가 0으로 표현되고 ❤️가 111로 표현됩니다.
(Case2) ❤️가 0으로 표현되고 🖕가 111로 표현됩니다.
당연히 연인끼리 ❤️를 쓸 확률(0.5)이 훨씬 많으므로 ❤️가 더 짧게 표현되는 (Case2)가 더 효율적인 코딩이 될 것입니다.
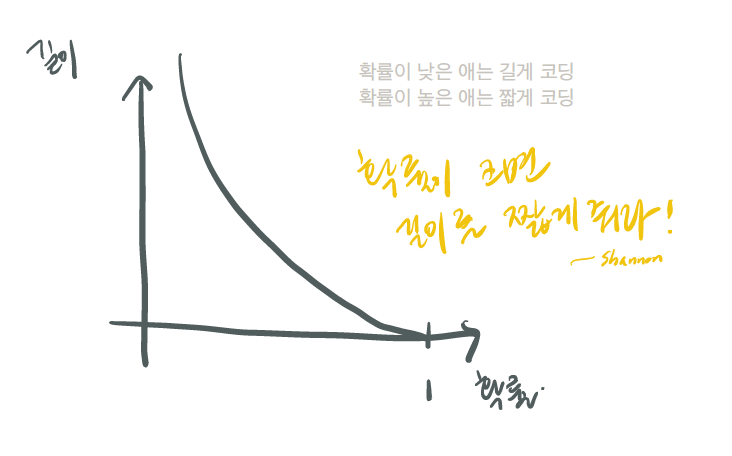
이와 같이 확률이 크면 길이를 짧게 주어야 한다는 것이 최소 평균 자원량으로 정보를 표현한다는 Entropy의 기본 개념입니다.

이제 이를 수식적으로 표현해보겠습니다. 로그함수를 거꾸로 표현한 것이기 때문에 -log를 취하고, bits로 표현되기 때문에 2가 붙습니다. 그리고 일어날 수 있는 각 사건(-log2Pi)에 대해 값을 구하고 다 더합니다. 이는 자원량의 최소 기댓값이 됩니다. 그리고 이 기댓값이 최소 평균 길이가 된다고 Shannon은 밝혔습니다.
Shannon는 논문에서 정보를 H로 표현하는데 수식으로 정리하면 아래와 같습니다.

추가적으로 모든 확률이 똑같을(uniform) 때 각 케이스의 길이가 같기 때문에 최소 기댓값이 가장 커지는 상황이 즉 entropy가 최대가 되는 상황이 발생하고 합니다. (최악의 상황)
Cross Entropy
그렇다면 Cross Entropy는 무엇이며, Entropy와 어떻게 다를까요?

Entropy는 '실제' 최소 길이라고 하면 Cross Entropy는 '내가 생각한' 최소 길이이라고 생각하면 됩니다. 그래서 Cross Entropy의 수식에서는 로그 뒤에 pi를 qi로 바꿔 표현하게 됩니다. 수식은 아래와 같습니다.

KL-divergence
앞서 설명한 '내가 생각한' 최소값(Cross Entropy)은 '실제' 최소값(Entropy)보다 당연히 더 크겠죠? 이렇게 더 값이 큰 것을 '비효율적'이라고 표현할 수 있습니다. 그리고 이 Entropy와 Cross Entropy의 차이가 '정보량의 차이'이며, 더 큰 값(Cross Entropy)에서 더 작은 값(Entropy)를 뺀 것을 KL-Divergence라고 합니다. 이를 간단하게 표현하면 이렇습니다.

이산형일 때와 연속형일 때를 모두 표현할 수 있는 정확한 식은 아래와 같습니다.

요약
- 실제 최소 정보량은 Entropy다.
- 내가 생각한 최소 정보량은 Cross Entropy다. 그리고 Entropy보다 크기 마련이다.
- Entropy와 Cross Entropy의 차이는 KL-divergence이다.
'Studies & Courses > Machine Learning & Vision' 카테고리의 다른 글
| [ML/DL] softmax와 negative log-likelihood (0) | 2021.01.10 |
|---|---|
| [ML/DL] 수포자가 이해한 Softmax (+Python 구현) (0) | 2021.01.09 |
| [ML/DL] 수포자가 이해한 2-Layer Neural Net의 vector form (0) | 2021.01.05 |
| [ML/DL] MNIST 손글씨 데이터 인식하기 (0) | 2020.12.31 |
| [ML/DL] 파이썬으로 인공 신경망 만들기 (1) | 2020.12.29 |




댓글