신경망 구축 과제에서 Loss 부분을 작성하는데 아래와 같은 Total Loss에 대한 정의가 있어 이 부분을 이해하고자 softmax와 log-likelihood에 대한 이해를 하고 넘어가고자 합니다.
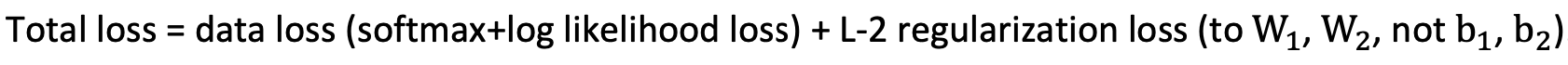
negative log-likelihood에 대한 더 직관적이고 빠른 이해가 필요할 때는 데이콘에서 제공한 강의에서 loss log에 대해 굉장히 쉽게 설명하고 있으니 참고하시면 좋을 것 같습니다.
log loss에 대해 알아보자 - [데이콘 평가산식]
이 포스팅에서는 softmax 함수, negative log-likelihood와 softmax 함수와의 관계 그리고 backpropagation을 할 때 derivative에 대해 알아보겠습니다.
- Softmax Activation Function
- Negative log-likelihood (NLL)
- Derivative of the Softmax
Softmax Activation Function
softmax는 multi-class learning problems에 쓰이며, 여기서 features set은 K class들 중 하나와 연결됩니다. 예를 들어 CIFA-10 image classification problem에서 pixel set이 input으로 주어지면, 우리는 특정 sample이 개와 고양이와 같은 class들 중 어디 하나에 속하는지를 classify해야 합니다.
equation은 간단하며, 우리는 layer 내 모든 units의 normalized exponential function을 계산하면 됩니다.
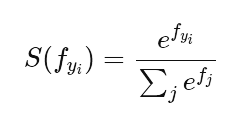
직관적으로 softmax는 0과 1사이에 size K의 vector를 쑤셔넣는(squash)역할을 한다고 보시면 됩니다.
그리고 exponential의 normalization이기 때문에, 모든 vector의 합은 1이 됩니다. 즉 어떤 feature set 이 어떤 class에 속할 확률을 나타낼 수 있습니다. 그래서 아래 3 class의 예시를 보면 forward propagation으로 score Yi가 계산됩니다. 그리고 softmax을 적용해 확률값을 얻습니다.

Negative Log-Likelihood (NLL)
실제 softmax을 쓸 때는 negative log-likelihood(NLL)와 사용됩니다. 이 loss function은 softmax와 관계에서 굉장히 흥미롭습니다. 우선, 우리의 loss function은 아래와 같습니다.

Parameter가 주어졌을 때 loss의 최소값을 찾아야 하기에 loss를 network의 '불행(unhappiness)'으로 해석해 봅시다. loss가 높을수록 '불행'지수가 높아지는 거겠죠? 우리는 이를 원하지 않습니다. 우리의 모델이 행복하길 바랍니다.
우리의 loss function을 negative log-likelihood로 사용하면, 이 loss function은 언제 불행하고 행복할까요?

위 그래프를 보면 input이 0일 때 무한으로 가고, input이 1일 때 0으로 갑니다. 이렇게 negative log-likelihood는 작은 값에서 불행하고 더 큰 값에서 덜 불행합니다. 정답 class에 대해서만 summing하기 때문에 실제로 network가 높은 confidence를 정답 class에 할당할 때마다 '불행'지수는 낮아집니다. 그러나 network가 낮은 confidence를 정답 class에 할당하면, '불행'지수는 높아집니다.

loss를 계산할 때 우리는 정답 class에 대한 높은 confidence가 낮은 loss로 이어지는 것을 볼 수 있습니다. 반대의 경우도 마찬가지고요. 예를 들어 hose의 confidence는 0.98으로 가장 높은데 Loss에서는 가장 낮은 0.02인 것은 볼 수 있습니다.
Derivative of the Softmax
이 파트에서는 softmax function을 negative log-likelihood에 대해 미분을 해볼 것입니다. 우리는 single example의 class scores를 포함하는 vector를 f라고 하고, 이는 network의 output입니다. 그래서 모든 j classes 내 어떤 class k의 원소를 fk라고 합시다. 그렇다면 우리는 softmax output을 아래와 같이 다시 쓸 수 있습니다.
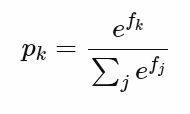
그리고 negative log-likelihood는 아래와 같습니다.

그리고 backpropagation을 perform하기 위해서 network의 output에 대한 loss의 변화량을 계산해야 합니다. L은 pk에 dependent하고, p는 fk에 dependent하기때문에그리고 backpropagation을 perform하기 위해서 network의 output에 대한 loss의 변화량을 계산해야 합니다.
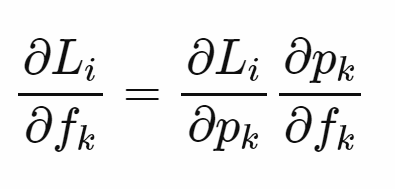
L은 pk에 dependent하고, p는 fk에 dependent하기때문에 우리는 이들을 chain rule로 표현할 수 있습니다.

첫 번째 미분은 위와 같이 log의 미분이고, 두 번째 미분은 quotient rule를 사용합니다. derivative를 operator D로 표현해봅시다.

DΣ가 efk가 되는 이유는 만약 input array f를 softmax function에서 취하면 우리는 언제나 k번째 element의 미분값을 취하기 때문입니다. 이 경우에 k번째 element에 대한 미분은 (efk인 elements 내에서) 언제나 0이 됩니다.
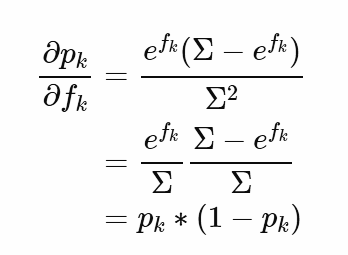
두 번째 미분을 완료하면 위와 같이 되며, 두 미분값을 combine하면 아래의 값을 얻을 수 있습니다.

이렇게 우리는 negative log likelihood를 softmax layer에 대해서 미분을 진행하였습니다.
(Sources)
ljvmiranda921.github.io/notebook/2017/08/13/softmax-and-the-negative-log-likelihood/
Understanding softmax and the negative log-likelihood
In this notebook I will explain the softmax function, its relationship with the negative log-likelihood, and its derivative when doing the backpropagation al...
ljvmiranda921.github.io
'Studies & Courses > Machine Learning & Vision' 카테고리의 다른 글
| [Coursera 수료 ✅ ] Neural Networks and Deep Learning (Notion/GitHub) (0) | 2021.02.08 |
|---|---|
| [cs231n] Minimal Neural Network Case Study (0) | 2021.01.14 |
| [ML/DL] 수포자가 이해한 Softmax (+Python 구현) (0) | 2021.01.09 |
| [ML/DL] 수포자가 이해한 Cross Entropy와 KL-divergence (0) | 2021.01.08 |
| [ML/DL] 수포자가 이해한 2-Layer Neural Net의 vector form (0) | 2021.01.05 |




댓글