[ML/DL] 수포자가 이해한 Softmax (+Python 구현)

*본 포스팅은 중학교 때 수학을 놓아버린 수포자가 기계학습을 이해하기 위해 정리한 것이므로 정확한 정보가 아닐 수 있습니다. 잘못된 정보는 댓글로 알려주시면 감사하겠습니다.

 

신경망 구현 과제의 TODO #2를 하기 위해서 Softmax classifier를 이해하고 Softmax classifier loss를 계산하는 forward pass 코드를 작성해야 합니다. 그래서 Softmax classifier loss가 무엇이며, python에서는 어떻게 표현되는지 알아보려고 합니다. 

 

logistic function / sigmoid function / softmax function 

 

시그모이드 함수는 로지스틱 함수라고 부르기도 하며, 로지스틱 함수의 한 케이스라 볼 수 있습니다. 인풋이 하나일 때 사용되는 시그모이드 함수를 인풋이 여러개일 때도 사용할 수 있도록 일반화 한 것이 소프트맥스 함수입니다.

 

즉 softmax와 sigmoid는 값의 개수가 다릅니다. sigmoid는 활성화 함수로 중간층에서 주로 이진분류를 위해 쓰이고, softmax는 출력층에 있어 다분류 출력이 가능합니다.  

 

활성화 함수 종류

 

Softmax+ Log Likelihood Loss =  Softmax Classifier

구분	sigmoid	softmax
목적	binary classification	multiclass(multinomial) classification
용도	주로 중간 층의 활성화 함수	주로 출력함수
출력 값 범위	0~1 사이의 확률값	0~1 사이의 확률값 (결과 총합 = 1)
출력 값 의미	ex. 0.5이상이면 양성, 이하면 음성의 의미	하나의 값에 대해 여러개(2개이상)클래스에 분류될 확률이 각 각 출력

 

---

Softmax 알고리즘의 이해

위의 표에서 볼 수 있듯이 softmax는 binary classification가 아닌 multiclass classification이 위의 표에서 볼 수 있듯이 softmax는 binary classification가 아닌 multiclass classification를 지원합니다. 여러 개의 연산 결과를 정규화하여 모든 클래스의 확률값의 합이 1이 됩니다. 아래의 케이스를 보면 (2.0, 1.0, 0.1)라는 점수를 정규화해 확률 값의 총합이 1이 되는 것을 알 수 있습니다. 

 

---

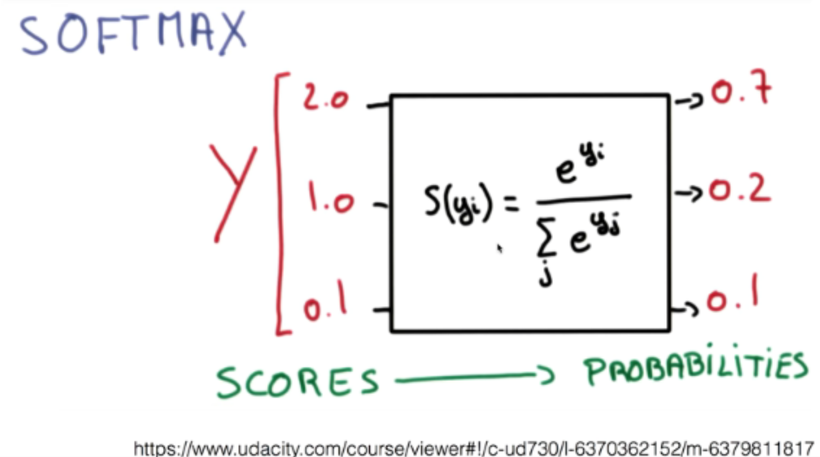
Softmax Classification의 Cost function

input parameter에 대한 우도를 평가하고 최대화하는 방법으로 cost function을 만들어냅니다. 입력 x와 그 정답 클래스의 쌍을 학습 데이터로 사용합니다. 그리고 일반적으로 Softmax classifier를 만들어내는 경우에는 정답 클래스를 one-hot encoding의 방법으로 학습시킵니다. 

위 그림에서 L은 정답 데이터이며, S(Y)는 실험 데이터일 것입니다. Cross-entropy를 통해 Cost가 최소가 되는 S의 값과 Y의 값을 찾아냅니다.  

 

---

Softmax를 Python 코드로 구현하기

COLAB

 

위 softmax 함수를 python으로 구형하면 아래와 같습니다. 

import numpy as np

def softmax(X):
	exp_a = np.exp(X)
    sum_exp_a = np.sum(exp_a)
    y = exp_a / sum_exp_a
    
    return y

그리고 이를 한 줄씩 실행하면 아래와 같습니다. 

 

 

위 코드는 잘 구현이 되지만 softmax 수식은 e의 지수를 포함하고 있고 이 지수함수는 지수가 커질 수록 큰 폭으로 증가(exponential)합니다. 예를 들어 exp(10)는 20,000넘고, exp(10)은 0이 40개가 넘는 큰 값이 되며, exp(1000)은 무한대를 뜻하는 inf가 return됩니다. 이렇게 큰 값끼리 나눗셈을 하면 결과가 불안정해집니다. 그래서 overflow 문제가 발생하기 쉽습니다. 

 

overflow는 컴퓨터가 표현할 수 있는 수의 범위가 한전되어, 너무 큰 값을 표현할 수 없는 문제를 의미합니다. 이를 개선하기 위해 softmax 식을 다음과 같이 변형합니다. 

 

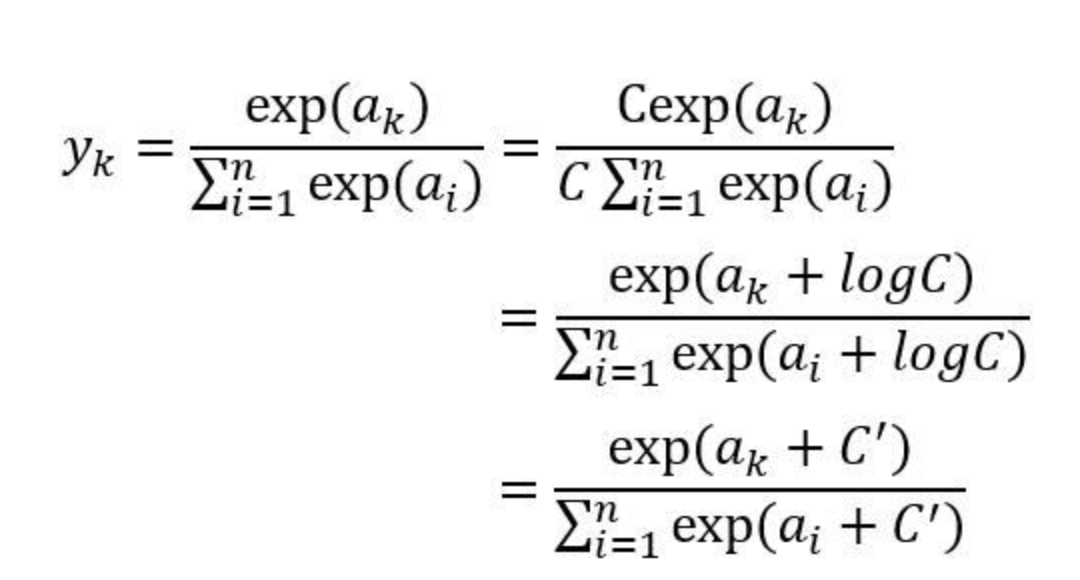
이는 원소에 어떤 수를 더하려 exp를 취하더라도 결과값이 같다는 softmax의 성질을 이용한 것입니다. 일반적으로 입력 신호 중 최댓값을 빼는 방식으로 합니다. 

 

예를 들어 a = [1010, 1000, 990]일 경우,  a-c는 [0, -10, -20]이 됩니다.

이를 함수로 표현하면 아래와 같습니다. 

 

def new_softmax(a) : 
    c = np.max(a) # 최댓값
    exp_a = np.exp(a-c) # 각각의 원소에 최댓값을 뺀 값에 exp를 취한다. (이를 통해 overflow 방지)
    sum_exp_a = np.sum(exp_a)
    y = exp_a / sum_exp_a
    return y

 

 

(참고)

 

 

deepnotes.io/softmax-crossentropy

Classification and Loss Evaluation - Softmax and Cross Entropy Loss

financial-engineering.medium.com/ml-softmax-%EC%86%8C%ED%94%84%ED%8A%B8%EB%A7%A5%EC%8A%A4-%ED%95%A8%EC%88%98-2f4740141bfe

[ML]Softmax 소프트맥스 함수

yamalab.tistory.com/87

Softmax Classifier의 이해 & Python으로 구현하기

blog.naver.com/hobbang143/221735605346

[머신러닝 - 18] 다중 분류(Multinomial Classification)와 소프트맥스(SoftMax)

blog.naver.com/th9231/221989350922

#수학 : 시그모이드 함수(Sigmoid) / 소프트맥스함수(Softmax)

leedakyeong.tistory.com/entry/%EB%B0%91%EB%B0%94%EB%8B%A5%EB%B6%80%ED%84%B0-%EC%8B%9C%EC%9E%91%ED%95%98%EB%8A%94-%EB%94%A5%EB%9F%AC%EB%8B%9D-%EC%86%8C%ED%94%84%ED%8A%B8%EB%A7%A5%EC%8A%A4-%ED%95%A8%EC%88%98-%EA%B5%AC%ED%98%84%ED%95%98%EA%B8%B0-in-%ED%8C%8C%EC%9D%B4%EC%8D%AC-softmax-in-python

[밑바닥부터 시작하는 딥러닝] 소프트맥스란? 소프트맥스 함수 구현하기 in 파이썬 (softmax in python

3months.tistory.com/66

Deep Learning - Softmax 구현 및 성질

kejdev.tistory.com/41

파이썬 클래스로 신경망 구현하기(cross_entropy, softmax, Softmax With loss )