Contents
- 선형 배열(Linear Array)
- 정렬(Sort)
- 탐색(Search)
- 재귀 알고리즘
- 동적계획법
- 연결리스트
- 양방향 연결리스트
- 스택
- 큐
- 환형큐
- 우선순위 큐
- 이진 트리
- 이진 탐색 트리
- 힙
선형 배열(Linear Array)
#Python 리스트에 활용할 수 있는 연산들
(1) 리스트 길이과 관계 없이 빠르게 실행 결과를 보게되는 연산들
- 원소 덧붙이기 .append()
- 원소 하나를 꺼내기 .pop()
(2) 리스트의 길이에 비례해서 실행 시간이 걸리는 연산들
- 원소 삽입하기 .insert()
- 원소 삭제하기 .del()
#리스트에서 원소 찾아내기
Example 1:
Input:
L = [64, 72, 83, 72, 54]
x = 72
Output:
[1, 3]
Example 2:
Input:
L = [64, 72, 83, 72, 54]
x = 83
Output:
[2]
Example 3:
Input:
L = [64, 72, 83, 72, 54]
x = 49
Output:
[-1]
Solution 1:
def solution(L,x):
result = list()
for i in range(len(L)):
if L[i] == x:
result.append(i)
if result == []:
result = [-1]
return result
정렬 (Sort)
#알파벳, 숫자 크기 순으로 정렬
L=['abcd','xyz','spam']
sorted(L)
#Out: ['abcd', 'spam', 'xyz']L=[3,7,2,7,1,7]
L.sort()
L
#Out: [1, 2, 3, 7, 7, 7]
#lambda : 익명함수
(lambda x,y: x + y)(5, 6)
#Out: 11
#정렬의 순서를 반대로
L=[3,4,2,0,1,8]
L2 = sorted(L,reverse=True)
L2
#Out: [8, 4, 3, 2, 1, 0]L=[3,4,2,0,1,8]
L.sort(reverse=True)
L
#Out: [8, 4, 3, 2, 1, 0]
#튜플의 정렬
a = [(1, 2), (0, 1), (5, 1), (5, 2), (3, 0)]
sorted(a, key = lambda x : x[0])#튜플 앞에 숫자의 크기가 작은 순서대로 정렬
#Out: [(0, 1), (1, 2), (3, 0), (5, 1), (5, 2)]
a = [(1, 2), (0, 1), (5, 1), (5, 2), (3, 0)]
sorted(a, key = lambda x : x[1]) #튜플 뒤에 숫자의 크기가 작은 순서대로 정렬
#[(3, 0), (0, 1), (5, 1), (1, 2), (5, 2)]
#길이 순서대로 정렬
L = ['abcd','xyz','spam']
sorted(L,key=lambda x: len(x)) #길이순서대로 정렬
#Out: ['xyz', 'abcd', 'spam']
#키를 지정하여 딕셔너리 정렬
L = [{'name':'John','score':83},{'name':'Paul', 'score':92}]
L.sort(key=lambda x:x['name']) #이름 순으로 정렬
L
#Out: [{'name': 'John', 'score': 83}, {'name': 'Paul', 'score': 92}]L = [{'name':'John','score':90},{'name':'Paul', 'score':50}]
L.sort(key=lambda x:x['score']) #점수 순으로 정렬
L
#Out: [{'name': 'Paul', 'score': 50}, {'name': 'John', 'score': 90}]
탐색 (Search)
#선형탐색 (Linear Search)
def linear_search(L,x):
i=0 #index i를 0으로 준다
while i < len(L) and L[i] != x: #i가 L리스트의 길이보다 작고, L의 i번째 원소가 x와 같지 않을때
i += 1 #i를 1씩 증가시켜나간다.
#원소가 발견되면 i값을 가지고 loop가 종료하게 될 것이기 때문에
#i가 L리스트의 길이보다 짧으면 리스트 안에서 원소를 발견했다는 의미
if i < len(L):
return i #발견된 x를 리턴하고
else:
return -1 #그렇지 않으면 -1을 리턴한다.
S = [3,8,2,7,6,7,6,10,9]
linear_search(S,6)
#Out: 4
S = [3,8,2,7,6,7,6,10,9]
linear_search(S,1)
#Out: -1
#이진 탐색 (Binary Search)
-Divide & Conquer : 정렬되어 있을때만 가능 → O(log n)
#이미 정렬된 리스트 L에서 x를 이진 탐색으로 찾기
#리스트에 없을 경우 -1 반환
def solution(L, x):
answer = -1
lt=0
rt=len(L)-1
while lt<=rt:
mid = (lt+rt)//2
if L[mid] == x:
answer = mid
break
elif L[mid]>x:
rt=mid-1
else:
lt=mid+1
return answer
#L 리스트 내 n개 숫자 중 target 위치를 이분 검색으로 찾기
n, target = map(int,input().split())
L = list(map(int,input().split()))
L.sort() #L을 순차로 정렬
lt=0 #lt는 가장 왼쪽 위치
rt=n-1 #lt는 가장 오른쪽 위치
while lt<=rt:
mid = (lt+rt)//2 #중간 값을 구함 : 몫을 구함
if L[mid] == target: #mid가 target이면 답을 찾은 것
print(mid+1) #mid는 index(0번 부터 시작)이기 때문에 +1
break
elif L[mid]>target:
#mid가 target보다 크면 lt...target..mid ...rt
#mid 왼쪽 탐색
rt=mid-1 #mid index에서 -1함으로써 mid보다 큰 쪽을 다 날림. rt가 mid-1값으로 조정됨
else:
#mid가 target보다 작면 lt.....mid ..target..rt
#mid 오른쪽 탐색
lt=mid+1 #mid위치에서 +1함으로써 mid+1위치부터 오른쪽으로 탐색
#Iput: 8 32
#Iput: 23 87 65 12 57 32 99 81
#Out: 3 (정렬 후의 결과이므로 작은 수로부터 3번째 큰 자리가 출력됨)
재귀 알고리즘 (recursive algorithms)
#종결조건의 중요성 알아보기
#재귀의 간단한 예시 - 1부터 n까지 sum
def sum(n):
print(n)
if n<=1: #이 종결 조건이 없으면 에러 발생 (계속 작아짐)
return n
else:
return n+sum(n-1)
a = int(input("Numer:"))
print(sum(a))
#In: 4
#Out:
#Numer:4
#4
#3
#2
#1
#10
#Recursive vs Iterative 복잡도
#recursive
def sum(n):
if n<=1:
return n
else:
return n+sum(n-1)#iterative
def sum(n):
s = 0
while n >=0:
s+=n
n-=1
return s- Recursive와 Iterative 모두 n에 비례하는 복잡도를 가짐 → O(n)
- 그러나 효율성 측면에서는 Recursive가 더 떨어질 수 있음
def sum(n):
return n*(n+1)//2
#O(1) 복잡도를 가짐
#Recursive 예제 - n!
#n!을 구하는 재귀함수
def factorial(n):
if n<=1:
return 1
else:
return n*factorial(n-1)
#Recursive vs Iterative 예제 - 피보나치(Fibonacci) 순열
#Recursive
def solution(n):
'''
F0 = 0
F1 = 1
Fn = Fn - 1 + Fn - 2, n >= 2
'''
if n <= 0:
return 0
elif n == 1:
return 1
else:
return solution(n-1)+solution(n-2)
solution(7)
#[1]1 - [2]1 - [3]2 - [4]3 - [5]5 - [6]8 - "[7]13"
#[5]8 + [6]8 = "[7]13"
#Out: 13
solution(8)
#[1]1 - [2]1 - [3]2 - [4]3 - [5]5 - [6]8 - [7]13 - "[8]21"
#[6]8 +[7]13 = "[8]21"
#Out: 21
#Iteratvie
def solution(n):
if n < 2:
return n
a, b = 0, 1
for i in range(n):
a, b = b, a+b
return a
solution (4)
solution (8)
#[1]a,b=1,1
#[2]a,b=1,2
#[3]a,b=2,3
#[4]a,b=3,5
#[5]a,b=5,8
#[6]a,b=8,13
#[7]a,b=13,21
#[8]a,b=21,34
#a = 21
#Out: 21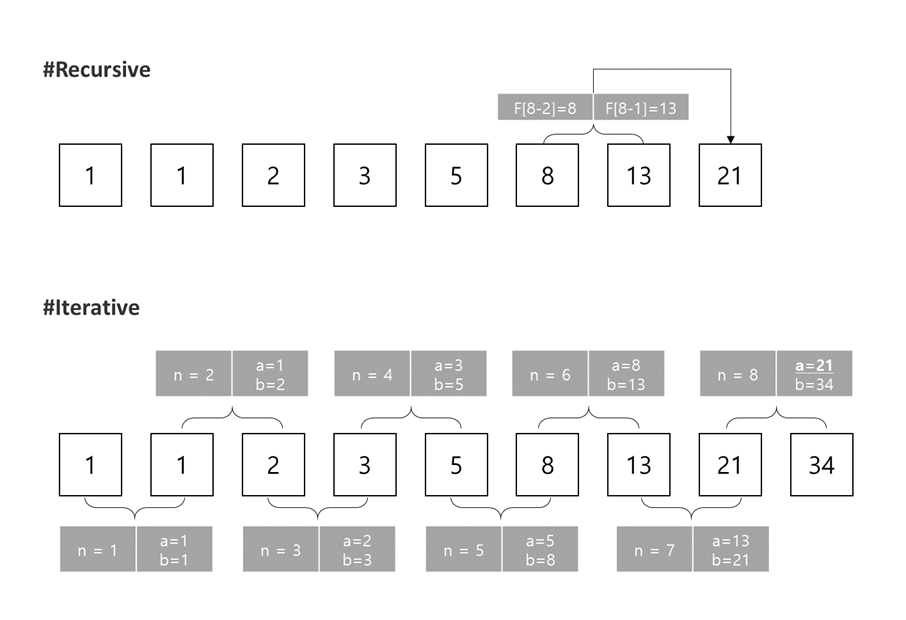
#Recursive 예제 - 조합의 수 계산
#재귀적 방법으로 조합의 수 계산
#n개의 다른 원소에서 m개를 택하는 경우의 수
def combi(n, m):
#if와 elif를 이용해 trivial case
if n == m: #선택하는 원소의 개수가 전체 원소의 개수와 같으면
return 1 #1로 반환
elif m == 0: #선택하는 원소 개수가 없으면
return 1 #1로 반환
else:
return combi(n-1,m)+combi(n-1,m-1)
#Recursive 예제 - 이진탐색
#L은 리스트
#x는 찾으려는 원소
#l부터 u까지 리스트 내 범위 인덱스
def solution(L, x, l, u):
if l > u:
return -1
mid = (l + u) // 2
if x == L[mid]:
return mid
elif x < L[mid]: x가 mid보다 작을 경우
return solution(L, x, l, mid-1) #mid의 오른쪽 날림
else:
return solution(L, x, mid+1, u) #mid의 왼쪽 날림
동적계획법(Dynamic programming)
#동적계획법(Dynamic programming)
- 복잡한 문제를 간단한 여러 개의 문제로 나누어 푸는 방법 (wikipedia)
- Bottom-Up 적 방법
#동적계획법 예제 - nm선 자르기
#nm의 선을 1m나 2m 자르는 방법의 수
#1m 선의 경우
#[1,1,1] => 1가지
#dy[1]=1
#2m 선의 경우
#[1,1,1],[2] => 2가지
#dy[2]=2
#3m 선의 경우
#[1,1,1] => 1가지
#[1,1,1],[2] => 2가지
#1가지(1m선의 경우) + 2가지(2m선의 경우) = 3가지
#dy[3]=3
#4m 선의 경우
#2가지(2m선의 경우) + 3가지(3m선의 경우) = 5가지
#dy[4]=5
n = int(input())
dy=[0]*(n+1) #배열을 만듦
dy[1]=1
dy[2]=2
for i in range(3, n+1): #3부터 n+1 범위 계산
dy[i] = dy[i-1]+dy[i-2]
print(dy[n])
#Brute Force 접근법
: 가능한 부분 배열들을 모두 살펴본 후 합을 구해서 가장 큰 값을 찾는 방식
#카데인 알고리즘 (Kadane’s Algorithm)
: A[0]이 아닌 A[n-1]에서(뒤에서 부터) 시작하는 방식
#카데인 알고리즘 (Kadane’s Algorithm) 예제 - Maximum Subarray Problem(최대 부분 합 구하기)
Input: nums = [-2,1,-3,4,-1,2,1,-5,4]
Output: 6
Explanation: [4,-1,2,1] has the largest sum = 6.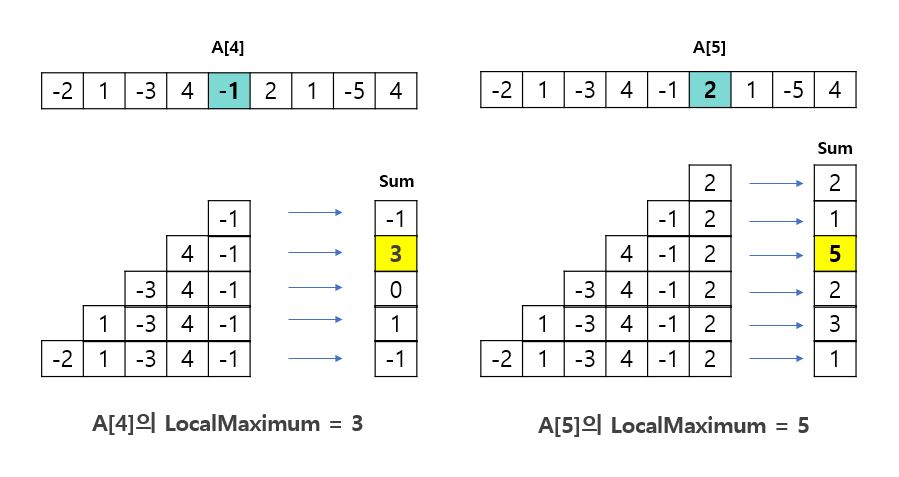
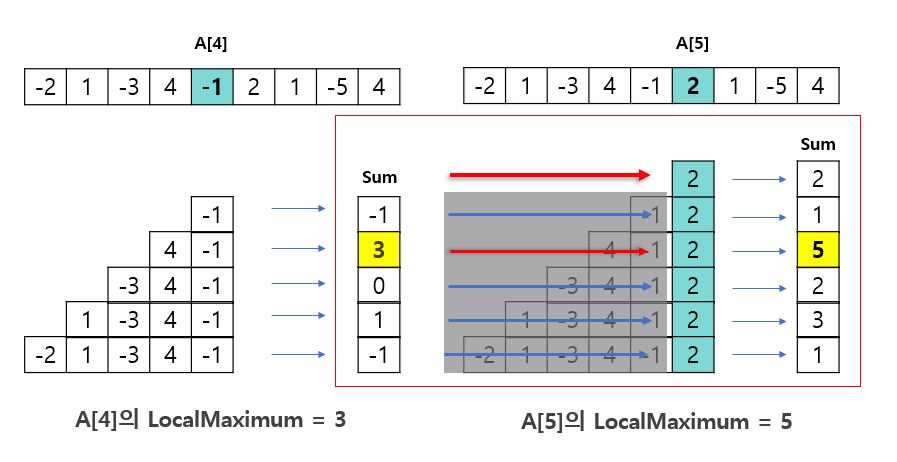
A[5]의 최대 부분합 = A[4]의 최대 부분합+A[5] = 3+2 = 5
A[6]의 최대 부분합 = A[5]의 최대 부분합+A[6] = 5+1 = 6
A[7]의 최대 부분합 = A[6]의 최대 부분합+A[7] = 5-5 = 0
A[8]의 최대 부분합 = A[7]의 최대 부분합+A[8] = 0+4 = 4
localMaximum[i] = max(A[i], A[i] + lacalMaximum[i-1])
#i번째에서는 A의 i번째 수와 i-1번째의 최대 부분합을 더한다.
연결리스트 (Linked List)
#자료 구조 정의
#노드
class Node:
def __init__(self.item):
self.data = item
self.next = None
#비어있는 연결리스트
class LinkedList:
def __init(self)
self.nodeCount = 0
self.head = None
self.tail = None
#연산 정의
(1) 특정 원소 참조 (k번째)
#K번째 노드 찾기
#[1][67] -> [2][34] -> [3][58]
# 노드의 개수: 3
#Head: 67
#Tail: 58
def getAt(self, pos):
if pos <=0 or pos > self.nodeCount: #pos 번째에 있는 노드를 반환하는 것이 목표
retrun None #pos가 0보다 작거나 노드 개수보다 작으면 없다.
i = 1
curr = self.head
while i < pos:
curr = curr.next
i += 1
return curr
(2) 리스트 순회
def traverse(self):
if not self.head:
return []
returnList = []
curr = self.head # 1
while curr is not None:
returnList.append(curr.data) # 67
curr = curr.next
return returnList
(3) 길이 얻어내기
# Node class
class Node:
# Function to initialise the node object
def __init__(self, data):
self.data = data # Assign data
self.next = None # Initialize next as null
# Linked List class contains a Node object
class LinkedList:
# Function to initialize head
def __init__(self):
self.head = None
# This function is in LinkedList class. It inserts
# a new node at the beginning of Linked List.
def push(self, new_data):
# 1 & 2: Allocate the Node &
# Put in the data
new_node = Node(new_data)
# 3. Make next of new Node as head
new_node.next = self.head
# 4. Move the head to point to new Node
self.head = new_node
# This function counts number of nodes in Linked List
# iteratively, given 'node' as starting node.
def getCount(self):
temp = self.head # Initialise temp
count = 0 # Initialise count
# Loop while end of linked list is not reached
while (temp):
count += 1
temp = temp.next
return count
(4) 원소 삽입
#원소 삽입
def insertAt(self, pos, newNode):
if pos < 1 or pos > self.nodeCount + 1:#pos가 올바른 값을 가지는 범위에 없으면
return False #False를 반환함
if pos == 1: #삽입하려는 위치가 맨 앞일 때 prev가 없음
newNode.next = self.head #head 조정 필요
self.head =newNode
else: #삽입하려는 위치가 리스트의 처음이 아니라면
prev = self.getAt(pos - 1) #직전의 노드를 얻고
newNode.next = prev.next #삽입되는 노드의 next는 pos - 1 노드의 next로 보냄
prev.next = newNode #prev의 next링크는 newNode를 가르키도록 조정
if pos == self.nodeCount +1:#삽입하려는 위치가 맨 끝일때
self.tail = newNode #tail을 새로운 노드에 가르키도록 조정
self.nodeCount += 1 #self에 +1한 뒤 True를 반환
return True
#삽입하려는 위치가 맨 끝일때
def insertAt(self, pos, newNode):
if pos < 1 or pos > self.nodeCount + 1:#pos가 올바른 값을 가지는 범위에 없으면
return False #False를 반환함
if pos == 1: #삽입하려는 위치가 맨 앞일 때 prev가 없음
newNode.next = self.head #head 조정 필요
self.head =newNode
else:
if prev = self.getAt + 1:
prev = self.tail #prev가 self의 tail로
else:
prev = self.getAt(pos -1) #그렇지 않으면 앞에서부터
newNode.next = prev.next
prev.next = newNode
if pos == self.nodeCount +1:
self.tail = newNode
self.nodeCount += 1 #self에 +1한 뒤 True를 반환
return True- 원소 삽입 실습
class Node:
def __init__(self, item):
self.data = item
self.next = None
class LinkedList:
def __init__(self):
self.nodeCount = 0
self.head = None
self.tail = None
def __repr__(self):
if self.nodeCount == 0:
return 'LinkedList: empty'
s = ''
curr = self.head
while curr is not None:
s += repr(curr.data)
if curr.next is not None:
s += ' -> '
curr = curr.next
return s
def getAt(self, pos):
if pos < 1 or pos > self.nodeCount:
return None
i = 1
curr = self.head
while i < pos:
curr = curr.next
i += 1
return curr
def insertAt(self, pos, newNode):
if pos < 1 or pos > self.nodeCount + 1:
return False
if pos == 1:
newNode.next = self.head
self.head = newNode
else:
if pos == self.nodeCount + 1:
prev = self.tail
else:
prev = self.getAt(pos - 1)
newNode.next = prev.next
prev.next = newNode
if pos == self.nodeCount + 1:
self.tail = newNode
self.nodeCount += 1
return True
def getLength(self):
return self.nodeCount
def traverse(self):
result = []
curr = self.head
while curr is not None:
result.append(curr.data)
curr = curr.next
return result
def concat(self, L):
self.tail.next = L.head
if L.tail:
self.tail = L.tail
self.nodeCount += L.nodeCount
a = Node(67)
b = Node(34)
c = Node(28)
L = LinkedList()
L
#Out: LinkedList: empty
L.insertAt(1,a)
#Out: True
L.insertAt(2,b)
#Out: True
L
#Out: 67 -> 34
L.insertAt(1,c)
#Out: True
L
#Out: 28 -> 67 -> 34- 원소 삽입의 복잡도
맨 앞에 삽입하는 경우 : O(1)
중간에 삽입하는 경우 : O(n)
맨 끝에 삽입하는 경우 : O(1)
(5) 원소 삭제
- 원소 삭제의 복잡도
맨 앞에 삭제하는 경우 : O(1)
중간에 삭제하는 경우 : O(n)
맨 끝에 삭제하는 경우 : O(n)
#연결 리스트 순회 예제
class Node:
def __init__(self, item):
self.data = item
self.next = None
class LinkedList:
def __init__(self):
self.nodeCount = 0
self.head = None
self.tail = None
def getAt(self, pos):
if pos < 1 or pos > self.nodeCount:
return None
i = 1
curr = self.head
while i < pos:
curr = curr.next
i += 1
return curr
def traverse(self):
if not self.head:
return []
returnList = []
curr = self.head
while curr is not None:
returnList.append(curr.data)
curr = curr.next
return returnList
# 이 solution 함수는 그대로 두어야 합니다.
def solution(x):
return 0
(6) 두 리스트 합치기
#두 리스트의 연결
def concat(self,L):
self.tail.next = L.head #내 끝이 이어 붙이려는 처음
#내 tail이 이어붙이려는 tail
#L.tail이 유효한 경우에만 붙임
if L.tail
self.tail = L.tail
self.nodeCount +=L.nodeCount
#Dummy node를 추가한 형태
class Node:
def __init__(self, item):
self.data = item
self.next = None
class LinkedList:
def __init__(self):
self.nodeCount = 0
self.head = Node(None)
self.tail = None
self.head.next = self.tail
def __repr__(self):
if self.nodeCount == 0:
return 'LinkedList: empty'
s = ''
curr = self.head
while curr.next:
curr = curr.next
s += repr(curr.data)
if curr.next is not None:
s += ' -> '
return s
def getLength(self):
return self.nodeCount
#리스트 순회
def traverse(self):
result = []
curr = self.head
while curr.next: #next 링크가 살아있는 한
curr = curr.next
result.append(curr.data) #그 결과를 result리스트에 담는다.
return result
#K번째 원소 얻어내기
def getAt(self, pos):
if pos < 0 or pos > self.nodeCount:
return None #pos가 0보다 작으면 head 리턴
i = 0
curr = self.head
while i < pos:
curr = curr.next
i += 1
return curr
#원소의 삽입
#[prev]->[prev.next]
#[prev]->[newNode]->[prev.next]
def insertAfter(self, prev, newNode):
newNode.next = prev.next #newNode의 next링크는 prev.next
if prev.next is None: #prev.next가 없다면
self.tail = newNode #tail이 newNode로 옮겨짐
prev.next = newNode #prev가 가리키는 node의 다음에 newNode 삽입
self.nodeCount += 1
return True #성공/실패에 따라 True/False를 리턴
def insertAt(self, pos, newNode):
if pos < 1 or pos > self.nodeCount + 1:
return False
if pos != 1 and pos == self.nodeCount + 1:
prev = self.tail
else:
prev = self.getAt(pos - 1)
return self.insertAfter(prev, newNode)
def concat(self, L):
self.tail.next = L.head.next
if L.tail:
self.tail = L.tail
self.nodeCount += L.nodeCount
- 리스트 순회
#리스트 순회
def traverse(self):
result = []
curr = self.head
while curr.next: #next 링크가 살아있는 한
curr = curr.next
result.append(curr.data) #그 결과를 result리스트에 담는다.
return result
- 특정 원소 참조 (k번째)
#K번째 원소 얻어내기
def getAt(self, pos):
if pos < 0 or pos > self.nodeCount:
return None #pos가 0보다 작으면 head 리턴
i = 0
curr = self.head
while i < pos:
curr = curr.next
i += 1
return curr
#pos범위 조건 확인
def insertAt(self, pos, newNode):
if pos < 1 or pos > self.nodeCount + 1:
return False
#pos == 1인 경우에는 head 뒤에 새 node 삽입
#pos == nodeCount +1인 경우에는 prev <- tail
if pos != 1 and pos == self.nodeCount + 1:
prev = self.tail
#그렇지 않은 경우에는 prev <- getAt(...)
else:
prev = self.getAt(pos - 1)
return self.insertAfter(prev, newNode)
- 원소 삽입
#원소의 삽입
#[prev]->[prev.next]
#[prev]->[newNode]->[prev.next]
def insertAfter(self, prev, newNode):
newNode.next = prev.next #newNode의 next링크는 prev.next
if prev.next is None: #prev.next가 없다면
self.tail = newNode #tail이 newNode로 옮겨짐
prev.next = newNode #prev가 가리키는 node의 다음에 newNode 삽입
self.nodeCount += 1
return True #성공/실패에 따라 True/False를 리턴
- 원소 삭제
def popAt(self, pos):
data = 0
if pos < 1 or pos > self.nodeCount:
raise IndexError
if self.nodeCount == 1:
data = self.head.data
self.head = None
self.tail = None
else:
if pos == 1:
data = self.head.data
self.head = self.head.next
if pos == self.nodeCount:
prev = self.getAt(pos-1)
data = prev.next.data
prev.next = None
self.tail = prev
else:
prev = self.getAt(pos-1)
data = prev.next.data
prev.next = prev.next.next
self.nodeCount -= 1
return data
- 두 리스트 합치기
#두 리스트의 연결
def concat(self, L):
self.tail.next = L.head.next
if L.tail:
self.tail = L.tail
self.nodeCount += L.nodeCount
연결리스트 (Linked List)
#Node의 구조 확장
#<-[]->
class Node:
def __init__(self, item):
self.data = item
self.prev = None
self.next = None
#Dummy node
class DoublyLinkedList:
def __init__(self):
self.nodeCount = 0
self.head = Node(None)
self.tail = Node(None)
self.head.prev = None
self.head.next = self.tail
self.tail.prev = self.head
self.tail.next = None
#리스트 순회
def traverse(self):
result = []
curr = self.head
while curr.next.next: #Dummy Node가 head와 tail에 모두 있음
curr = curr.next #빈 리스트라도 순회
result.append(curr.data)
return result
#리스트 역순회
def revese(self):
result = []
curr = self.head
while curr.prev.prev: #prev > prev
curr = curr.prev #빈 리스트라도 반복하지 않고 빠져 나옴> 유효함
result.append(curr.data)
return result
#원소의 삽입
def insertBefore(self, next, newNode):
prev = next.prev
newNode.next = prev.next
newNode.prev = prev
prev.next = newNode
next.prev = newNode
self.nodeCount += 1
return True#링크만 조정하면 됨
def insertAfter(self, prev, newNode):
next = prev.next
newNode.prev = prev
newNode.next = next
prev.next = newNode
next.prev = newNode
self.nodeCount += 1
return True
#특정 원소 얻어내기
def getAt(self, pos):
if pos < 0 or pos > self.nodeCount:
return None
if pos > self.nodeCount // 2:
i = 0
curr = self.tail #뒤에서 하나하나 세도록
while i < self.nodeCount - pos + 1:
curr = curr.prev
i += 1
else:
i = 0
curr = self.head
while i < pos:
curr = curr.next
i += 1
#양방향 연결 리스트 노드 삭제
def popAfter(self, prev):
curr = prev.next
prev.next = curr.next
curr.next.prev = prev
self.nodeCount -= 1
return curr.data
def popBefore(self, next):
curr = next.prev
prev = curr.prev
prev.next = next
next.prev = prev
self.nodeCount -= 1
return curr.data
def popAt(self, pos):
if pos < 1 or pos > self.nodeCount:
raise IndexError
prev = self.getAt(pos - 1)
return self.popAfter(prev)
#양방향 연결 리스트의 병합
def concat(self, L):
self.tail.prev.next = L.head.next
L.head.next.prev = self.tail.prev
self.tail = L.tail
self.nodeCount += L.nodeCount
스택(Stacks)

#연산의 정의
- size(): 현재 스택에 들어 있는 데이터 원소의 수를 구함
- isEmpty(): 현재 스택이 비어 있는지를 판단 (size() == 0?)
- push(x): 데이터 원소 x 를 스택에 추가
- pop(): 스택에 가장 나중에 저장된 데이터 원소를 제거 (또한, 반환)
- peek(): 스택에 가장 나중에 저장된 데이터 원소를 참조 (반환), 그러나 제거하지는 않음
#배열로 구현한 스택
class ArrayStack:
def __init__(self):
self.data = []
def size(self): #크기 리턴
return len(self.data)
def isEmpty(self):
return self.size() == 0
def push(self, item):
self.data.append(item)
def pop(self): #원소 삭제(리턴)
return self.data.pop()
def peek(self): #꼭대기 원소 반환
return self.data[-1]
#양방향연결리스트로 구현한 스택
from doublylinkedlist import Node
from doublylinkedlist import DoublyLinkedList
class LinkedListStack:
def __init__(self):
self.data = DoublyLinkedList()
def size(self):
return self.data.getLength()
def isEmpty(self):
return self.size() == 0
def push(self, item):
node = Node(item)
self.data.insertAt(self.size() + 1, node) #1만큼 사이즈가 늘어난 뒤 추가
def pop(self):
return self.data.popAt(self.size())
def peek(self):
return self.data.getAt(self.size()).data
#수식의 후위 표기법 (Postfix Notation)
- 연산자가 피연산자들의 뒤에 위치
| 중위 | 후위 |
| A*B+C | A+B*C |
| AB*C+ | ABC*+ |
| A+B+C | AB+C+ |
| (A+B)*C | AB+C* 여는 괄호는 스택에 push 닫는 괄호를 만나면 여는 괄호가 나올 때까지 pop |
| A*(B+C) | ABC+** 연산자를 만났을 떄 여는 괄호 너머까지 pop하지 않도록 여는 괄호의 우선순위는 가장 낮게 설정 |
| (A+B) * (C+D) | AB+CD+* |
| (A+(B-C))*D | ABC-+D* |
| A*(B-(C+D)) | ABCD+-* |
- 중위 표현식 왼쪽부터 한 글자씩 읽어서 피연산자이면 그냥 출럭
- '('이면 스택에 push
- ')'이면 '('이 나올 때까지 스택에서 pop, 출력
- 연산자이면 스택에서 이보다 높거나 같은 우선순위 것들을 pop, 출력
- 이 연산자는 스택에 push하고 스택에 남아 있는 연산자는 모두 pop, 출력중위표현 수식 --> 후위표현 수식
#중위표현 수식 → 후위표현 수식 예제
class ArrayStack:
def __init__(self):
self.data = []
def size(self):
return len(self.data)
def isEmpty(self):
return self.size() == 0
def push(self, item):
self.data.append(item)
def pop(self):
return self.data.pop()
def peek(self):
return self.data[-1]
prec = {
'*': 3, '/': 3,
'+': 2, '-': 2,
'(': 1
}
def solution(S):
stack = []
answer = ''
for c in S:
if c not in '()+-*/':
answer += c
elif c == '(':
stack.append(c)
elif c == ')':
while stack[-1] != '(':
answer += stack.pop()
stack.pop()
elif stack and prec[c] <= prec[stack[-1]]:
answer += stack.pop()
stack.append(c)
else:
stack.append(c)
while stack:
answer += stack.pop()
return answer
#후위 표기 수식 계산
def postfixEval(tokenList):
valStack = ArrayStack()
for token in tokenList:
if type(token) is int:
valStack.push(token)
elif token == '+':
n1 = valStack.pop()
n2 = valStack.pop()
valStack.push(n2+n1)
elif token == '-':
n1 = valStack.pop()
n2 = valStack.pop()
valStack.push(n2-n1)
elif token == '*':
n1 = valStack.pop()
n2 = valStack.pop()
valStack.push(n2*n1)
elif token == '/':
n1 = valStack.pop()
n2 = valStack.pop()
valStack.push(int(n2/n1))
return valStack.pop()
큐 (Queue)

#연산의 정의
- size() : 현재 큐에 들어있는 데이터 원소의 수를 구함
- isEmpty() : 현재 큐가 비어 있는지를 판단
- enqueue(x) : 데이터 원소 x를 큐에 추가
- dequeue() : 큐의 맨 앞에 저장된 데이터 원소를 제거(또는 반환)
- peek() : 큐의 맨 앞에 저장된 데이터 원소를 반환(제거하지 않음)
#배열을 이용하여 구현
class ArrayQueue:
def __init__(self):
self.data = []
def size(self):
return len(self.data)
def isEmpty(self):
return self.size() == 0
def enqueue(self, item):
self.data.append(item)
def dequeue(self):
return self.data.pop(0)
def peek(self):
return self.data[0]
| 연산 | 복잡도 |
| size() | O(1) |
| isEmpty() | O(1) |
| enqueue() | O(1) |
| dequeue() | O(n) |
| peek() | O(1) |
#이중 연결리스트을 이용하여 구현
class Node:
def __init__(self, item):
self.data = item
self.prev = None
self.next = None
class DoublyLinkedList:
def __init__(self):
self.nodeCount = 0
self.head = Node(None)
self.tail = Node(None)
self.head.prev = None
self.head.next = self.tail
self.tail.prev = self.head
self.tail.next = None
def __repr__(self):
if self.nodeCount == 0:
return 'LinkedList: empty'
s = ''
curr = self.head
while curr.next.next:
curr = curr.next
s += repr(curr.data)
if curr.next.next is not None:
s += ' -> '
return s
def getLength(self):
return self.nodeCount
def traverse(self):
result = []
curr = self.head
while curr.next.next:
curr = curr.next
result.append(curr.data)
return result
def reverse(self):
result = []
curr = self.tail
while curr.prev.prev:
curr = curr.prev
result.append(curr.data)
return result
def getAt(self, pos):
if pos < 0 or pos > self.nodeCount:
return None
if pos > self.nodeCount // 2:
i = 0
curr = self.tail
while i < self.nodeCount - pos + 1:
curr = curr.prev
i += 1
else:
i = 0
curr = self.head
while i < pos:
curr = curr.next
i += 1
return curr
def insertAfter(self, prev, newNode):
next = prev.next
newNode.prev = prev
newNode.next = next
prev.next = newNode
next.prev = newNode
self.nodeCount += 1
return True
def insertAt(self, pos, newNode):
if pos < 1 or pos > self.nodeCount + 1:
return False
prev = self.getAt(pos - 1)
return self.insertAfter(prev, newNode)
def popAfter(self, prev):
curr = prev.next
next = curr.next
prev.next = next
next.prev = prev
self.nodeCount -= 1
return curr.data
def popAt(self, pos):
if pos < 1 or pos > self.nodeCount:
raise IndexError('Index out of range')
prev = self.getAt(pos - 1)
return self.popAfter(prev)
def concat(self, L):
self.tail.prev.next = L.head.next
L.head.next.prev = self.tail.prev
self.tail = L.tail
self.nodeCount += L.nodeCountclass LinkedListQueue:
def __init__(self):
self.data = DoublyLinkedList()
def size(self):
return self.data.nodeCount
def isEmpty(self):
return self.data.nodeCount==0
def enqueue(self, item):
node = Node(item)
self.data.insertAt(self.size()+1,node)
def dequeue(self):
return self.data.popAt(1)
def peek(self):
return self.data.head.next.datadef solution(x):
return 0
#양방향 연결리스트을 이용한 큐 구현 예제
class Node:
def __init__(self, item):
self.data = item
self.prev = None
self.next = None
class DoublyLinkedList:
def __init__(self):
self.nodeCount = 0
self.head = Node(None)
self.tail = Node(None)
self.head.prev = None
self.head.next = self.tail
self.tail.prev = self.head
self.tail.next = None
def __repr__(self):
if self.nodeCount == 0:
return 'LinkedList: empty'
s = ''
curr = self.head
while curr.next.next:
curr = curr.next
s += repr(curr.data)
if curr.next.next is not None:
s += ' -> '
return s
def getLength(self):
return self.nodeCount
def traverse(self):
result = []
curr = self.head
while curr.next.next:
curr = curr.next
result.append(curr.data)
return result
def reverse(self):
result = []
curr = self.tail
while curr.prev.prev:
curr = curr.prev
result.append(curr.data)
return result
def getAt(self, pos):
if pos < 0 or pos > self.nodeCount:
return None
if pos > self.nodeCount // 2:
i = 0
curr = self.tail
while i < self.nodeCount - pos + 1:
curr = curr.prev
i += 1
else:
i = 0
curr = self.head
while i < pos:
curr = curr.next
i += 1
return curr
def insertAfter(self, prev, newNode):
next = prev.next
newNode.prev = prev
newNode.next = next
prev.next = newNode
next.prev = newNode
self.nodeCount += 1
return True
def insertAt(self, pos, newNode):
if pos < 1 or pos > self.nodeCount + 1:
return False
prev = self.getAt(pos - 1)
return self.insertAfter(prev, newNode)
def popAfter(self, prev):
curr = prev.next
next = curr.next
prev.next = next
next.prev = prev
self.nodeCount -= 1
return curr.data
def popAt(self, pos):
if pos < 1 or pos > self.nodeCount:
raise IndexError('Index out of range')
prev = self.getAt(pos - 1)
return self.popAfter(prev)
def concat(self, L):
self.tail.prev.next = L.head.next
L.head.next.prev = self.tail.prev
self.tail = L.tail
self.nodeCount += L.nodeCount
class LinkedListQueue:
def __init__(self):
self.data = DoublyLinkedList()
def size(self):
return self.data.nodeCount
def isEmpty(self):
return self.data.nodeCount==0
def enqueue(self, item):
node = Node(item)
self.data.insertAt(self.size()+1,node)
def dequeue(self):
return self.data.popAt(1)
def peek(self):
return self.data.head.next.data
def solution(x):
return 0
환형 큐(Circular Queue)

#환형 큐
- '정해진' 개수의 저장 공간을 빙 돌려가며 이용
- 큐가 가득 차면 더이상 원소를 넣을 수 없음
#연산의 정의
- size() : 현재 큐에 들어 있는 데이터 원소의 수를 구함
- isEmpty() : 현재 큐가 비어 있는지를 판단
- isFull() : 큐에 데이터 원소가 꼭 차 있는지를 판단
- qneueue(x) : 데이터 원소 x를 큐에 추가
- dequeue() : 큐의 맨 앞에 저장된 데이터 원소를 제거(또한, 반환)
- peek() : 큐의 맨 앞에 저장된 데이터 원소를 반환(제거하지 않음)
#배열로 구현한 환형 큐
class CircularQueue:
#큐 초기화
def __init__(self, n):
self.maxCount = n
self.data = [None] * n
self.count = 0
self.front = -1
self.rear = -1
# 현재 큐 길이를 반환
def size(self):
return self.count
# 큐가 비어있는지
def isEmpty(self):
return self.count == 0
# 큐가 꽉 차있는지
def isFull(self):
return self.count == self.maxCount
# 데이터 원소 추가
def enqueue(self, x):
if self.isFull():
raise IndexError('Queue full')
self.rear = (self.rear + 1) % self.maxCount
self.data[self.rear] = x
self.count += 1
#데이터 원소 제거
def dequeue(self):
if self.isEmpty():
raise IndexError('Queue empty')
self.front = (self.front + 1) % self.maxCount
x = self.data[self.front]
self.count -= 1
return x
# 큐의 맨 앞 원소 반환
def peek(self):
if self.isEmpty():
raise IndexError('Queue empty')
return self.data[(self.front + 1) % self.maxCount]
우선순위 큐 (Priority Queues)
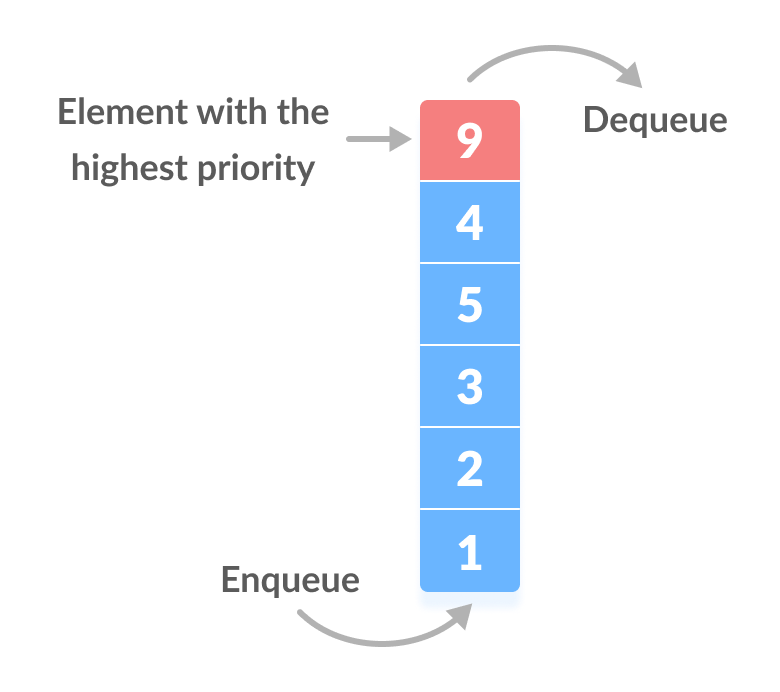
#우선순위 큐 (Priority Queues)
- 큐가 FIFO(First-In-First-Out) 방식을 따르지 않고 원소들의 우선순위에 따라 큐에서 빠져나오는 방식
#우선순위 큐 구현 방식
- (1) Enqueue할 때 우선순위 순서를 유지하도록 vs (2) Dequeue할 때 우선순위 높은 것을 선택
- (1) 가 더 유리, (2)는 모든 원소를 다 살펴보아야 함
#우선순위 큐 연상 구현
class PriorityQueue:
# 양방향 연결리스트를 이용하여 초기화
def __init__(self, x):
self.queue = DoublyLinkedList()
# 크기
def size(self):
return self.queue.getLength()
# 비어있는지
def isEmpty(self):
return self.size() == 0
# 데이터 삽입 연산
def enqueue(self, x):
newNode = Node(x)
# 처음 시작하는 위치 head에서 시작
curr = self.queue.head
# 끝까지 가지 않을 조건 && 우선순위를 비교하는 조건
while curr.next != self.queue.tail and x < curr.next.data :
curr = curr.next
# 양방향 연결리스트를 이용해 삽입
self.queue.insertAfter(curr, newNode)
# 데이터 삭제 연산
def dequeue(self):
return self.queue.popAt(self.queue.getLength())
# 첫번째 데이터 반환
def peek(self):
return self.queue.getAt(self.queue.getLength()).data
#우선순위 큐 연상 구현 예제
class PriorityQueue:
def __init__(self):
self.queue = DoublyLinkedList()
def size(self):
return self.queue.getLength()
def isEmpty(self):
return self.size() == 0
def enqueue(self, x):
newNode = Node(x)
curr =
self.queue.head
while
curr.next != self.queue.tail
and
x < curr.next.data
:
curr = curr.next
self.queue.
insertAfter
(curr, newNode)
def dequeue(self):
return self.queue.popAt(self.queue.getLength())
def peek(self):
return self.queue.getAt(self.queue.getLength()).data
def solution(x):
return 0
이진 트리 (Binary Trees)
#연산의 정의
-
size() : 현재 트리에 포함되어 있는 노드의 수를 구함
-
depth() : 현재 트리의 깊이(또는 높이;height)를 구함
-
순회(traversal)
#이진 트리의 구현 - size()
# 이진트리의 구현 - 노드(node)
class Node:
def __init__(self, item):
self.data = item
self.left = None
self.right = None
# 이진 트리의 구현 - 트리(tree)
class BinaryTree:
def __init__(self, r):
self.root = r
class Node:
# 이진 트리의 크기 - 재귀함수 이용
def size(self):
l = self.left.size() if self.left else 0 # 왼쪽 서브트리
r = self.right.size() if self.right else 0 # 오른쪽 서브트리
return l + r + 1 # 왼쪽 + 오른쪽 + 자기자신(+1)
class BinaryTree:
# 크기 구하기
def size(self):
if self.root:
return self.root.size()
else:
return 0
#이진 트리의 구현 - depth()
# depth
def depth(self):
l = self.left.depth() if self.left else 0
r = self.right.depth() if self.right else 0
return max(l,r) + 1
#깊이 우선 순회 (depth first traveral)
(1) 중위 순회 (in-order traversal) : Left subtree → 자기 자신 → Right subtree

# 중위 순회
def inorder(self):
traversal = []
# 왼쪽 서브트리가 존재한다면
if self.left:
traversal += self.left.inorder()
traversal.append(self.data)
# 오른쪽 서브트리가 있다면
if self.right:
traversal += self.right.inorder()
return traversal
(2) 전위 순회 (pre-order traversal) : 자기 자신 → Left subtree → Right subtree

def preorder(self):
traversal = []
traversal.append(self.data)
if self.left:
traversal += self.left.preorder()
if self.right:
traversal += self.right.preorder()
return traversal
(3) 후위 순회 (post-order traversal): Left subtree → Right subtree → 자기 자신

def postorder(self):
traversal = []
if self.left:
traversal += self.left.postorder()
if self.right:
traversal += self.right.postorder()
traversal.append(self.data)
return traversal
#넓이 우선 순회 (breadth first traversal)
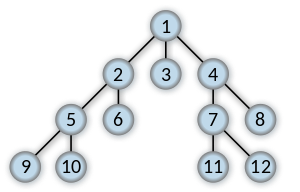
- 수준(Level)이 낮은 노드를 우선으로 방문
- 같은 수준의 노드들 사이에서는 부모 노드의 방문 순서에 따라 방문, 왼쪽 자식 노드를 오른쪽 자식보다 먼저 방문
- 한 노드를 방문했을 때, 나중에 방문할 노드들을 순서대로 기록해 두어야함
→ 선입선출 성질을 가지고 있기 때문에 자료구조는 큐를 사용
def bft(self):
# 빈 리스트 초기화
traversal = []
# 빈 큐 초기화
visitQueue = ArrayQueue()
# 빈 트리가 아니면 루트 노드가 있는 것 -> 큐에 루트 노드를 인큐
if self.root:
visitQueue.enqueue(self.root)
# 큐가 비어있지 않는 동안 반복
while visitQueue.isEmpty()==False:
# 큐에서 꺼내서 node에 저장
node = visitQueue.dequeue()
# 꺼낸 노드를 방문 리스트에 저장
traversal.append(node.data)
# 노드에 왼쪽 자식 노드가 존재하는경우 큐에 저장
if node.left:
visitQueue.enqueue(node.left)
# 노드에 오른쪽 자식 노드가 존재하는 경우 큐에 저장
if node.right:
visitQueue.enqueue(node.right)
return traversal
이진 탐색 트리 (Binary Search Trees)
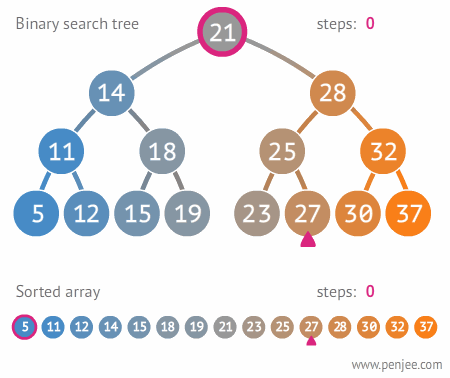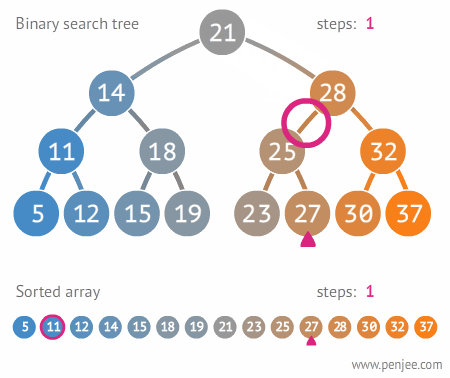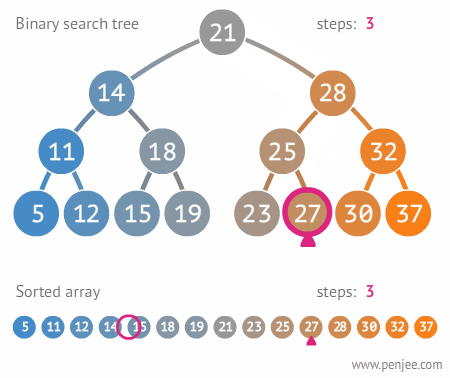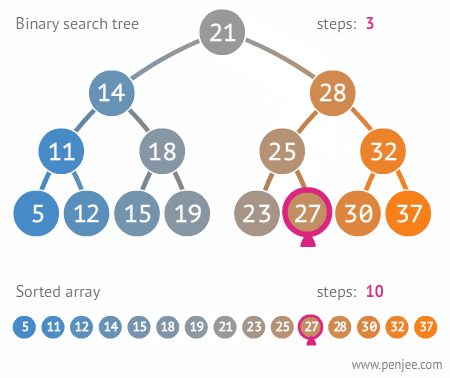
#이진 탐색 트리이진 탐색 트리 (Binary Searcah Trees)
- 왼쪽 서브트리에 있는 데이터는 모두 현재 노드의 값보다 작고, 오른쪽 서브트리에 있는 데이터는 모두 현재 노드의 값보다 큰 성질을 만족하는 이진트리 (중복되는 데이터 원소는 없는 것으로 가정)
#연산의 정의
- insert(key, data) : 트리에 주어진 데이터 원소를 추가
- remove(key) : 특정 원소를 트리로 부터 삭제
- lookup(key) : 특정 원소를 검색
- inorder() : 키의 순서대로 데이터 원소를 나열
- min(), max() : 최소 키, 최대 키를 가지는 원소를 각각 탐색
#insert(key, data)
class Node:
def insert(self, key, data):
if key < self.key:
if self.left:
self.left.insert(key, data)
else:
self.left = Node(key, data)
elif key > self.key:
if self.right:
self.right.insert(key, data)
else:
self.right = Node(key, data)
else:
print("중복된 노드가 존재")
return True
class BinSearchTree:
def insert(self, key, data):
if self.root:
self.root.insert(key,data)
else:
self.root = Node(key, data)
#remove(key)
def remove(self, key):
node, parent = self.lookup(key)
if node:
nChildren = node.countChildren()
if nChildren == 0:
if parent:
if parent.left == node:
parent.left = None
if parent.right == node:
parent.right = None
else:
self.root = None
#lookup()
def lookup(self, key, parent=None):
if key < self.key:
if self.left:
return self.left.lookup(key, self)
else:
return None, None
elif key > self.key:
if self.right:
return self.right.lookup(key, self)
else:
return None, None
else:
return self, parent
#inorder()
def inorder(self):
traversal = []
if self.left:
traversal += self.left.inorder()
traversal.append(self)
if self.right:
traversal += self.right.inorder()
return traversal
#min(), max()
def min(self):
if self.root:
return self.root.min()
else:
return None
def max(self):
if self.root:
return self.root.max()
else:
return None
#이진 탐색 트리의 원소 삽입 연산 구현
class Node:
def __init__(self, key, data):
self.key = key
self.data = data
self.left = None
self.right = None
def insert(self, key, data):
if key < self.key:
if self.left:
self.left.insert(key, data)
else:
self.left = Node(key,data)
elif key > self.key:
if self.right:
self.right.insert(key, data)
else:
self.right = Node(key, data)
else:
raise KeyError
return True
def inorder(self):
traversal = []
if self.left:
traversal += self.left.inorder()
traversal.append(self)
if self.right:
traversal += self.right.inorder()
return traversal
class BinSearchTree:
def __init__(self):
self.root = None
def insert(self, key, data):
if self.root:
self.root.insert(key, data)
else:
self.root = Node(key, data)
def inorder(self):
if self.root:
return self.root.inorder()
else:
return []
def solution(x):
return 0
#원소 삭제
(1) 방법
- 키(key)를 이용해서 노드를 찾는다
- 해당 키의 노드가 없으면 삭제할 것도 없음
- 노드가 있으면 찾은 노드의 부모 노드도 알고 있어야 함
- 찾은 노드를 제거하고도 이진 탐색 트리 성질을 만족하도록 트리의 구조를 정리함
(2) 인터페이스 설계
- 입력: 키(key)
- 출력: 삭제한 경우 True, 해당 키의 노드가 없는 경우 False
def remove(self, key):
node, parent = self.lookup(key)
if node:
...
return True
else:
return False(3) 이진 탐색 트리 구조의 유지
- 삭제되는 노드가 말단(leaf) 노드인 경우
: 그냥 그 노드를 없애면 됨
→ 부모 노드의 링크를 조정
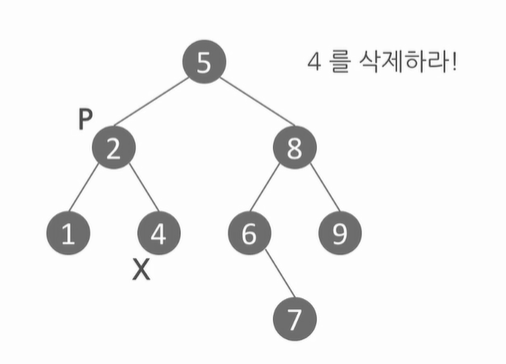

- 자식을 하나 가지고 있는 경우
: 삭제되는 노드 자리에 그 자식을 대신 배치
→ 자식이 왼쪽인지 오른쪽인지
→ 부모 노드의 링크를 조정 (좌/우 알고 있어야 함)
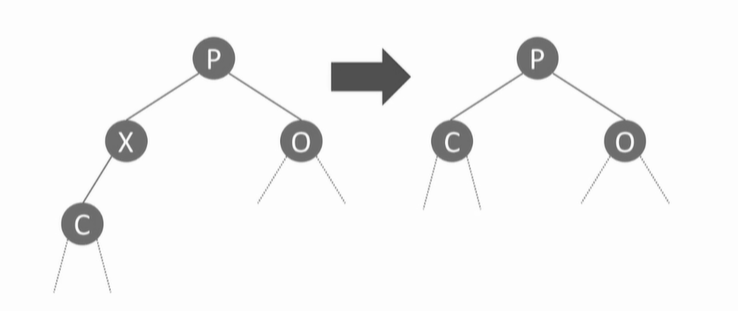

- 자식을 둘 가지고 있는 경우
: 삭제되는 노드보다 바로 다음 큰 키를 가지는 노드를 찾아 그 노드를 삭제되는 노드 자리에 대신 배치
→ 해당 노드를 삭제




#이진 탐색 트리가 효율적이지 못한 경우
- 순서대로 삽입하는 경우 효율적이지 못하다
- 한쪽으로 치우치는 모양
힙 (Heaps)

#힙과 이진 탐색 트리 비교
| 구분 | 힙 | 이진 탐색 트리 |
| 원소들은 완전히 크기 순으로 정렬되어 있는가? | X | O |
| 특정 키 값을 가지는 원소를 빠르게 검색할 수 있는가? | X | O |
| 부가의 제약 조건은 어떤 것인가? | 완전 이진 트리이어야 한다. |
#연산의 정의
- init() : 비어 있는 최대 힙을 생성
- insert(item) : 새로운 원소를 삽입
- remove() : 최대 원소(root node)를 반환하고 삭제
#배열을 이용한 이진 트리의 표현
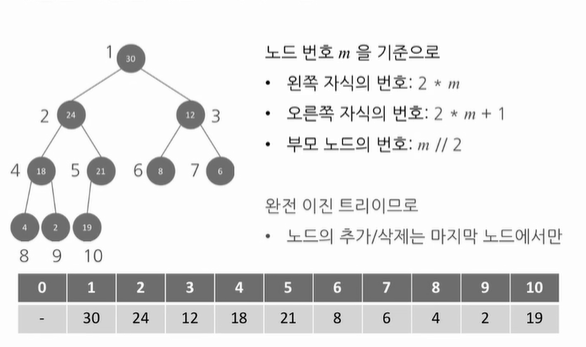
class MaxHeap:
def __init__(self):
self.data = [None]
#최대 힙에 원소 삽입
(1) 방법
- 트리의 마지막 자리에 새로운 원소를 임시로 저장
- 부모 노드의 키 값을 비교하여 위로, 비교하고 위로 이동
(2) 복잡도
- 원소의 개수가 n인 최대 힙에 새로운 원소 삽입
→ 부모 노드와 대소 비교 최대 회수: log2n
→ 최악 복잡도 O(logn)의 삽입 연산
#삽입 연산의 구현 - insert(item) 메서드
class MaxHeap:
def insert(self, item):
# 흰트 - python에서 두 변수의 값 바꾸기
# a = 3, b = 5
# a, b = b, a
self.data.append(item)
index = len(self.data) -1
while index != 1:
numOfParentNode = index//2
print(numOfParentNode)
if self.data[numOfParentNode] < self.data[index]:
self.data[numOfParentNode], self.data[index] = self.data[index], self.data[numOfParentNode]
index = numOfParentNode
else:
break
#최대 힙에서 원소의 삭제
(1) 방법
- 루트 노드의 제거 - 이것이 원소들 중 최대 값
- 트리 마지막 자리 노드를 임시로 루트 노드의 자리에 배치
- 자식 노드들과의 값 비교로 아래로, 비교하여 아래로 이동
→ 자식은 둘이 있을 수 있는데 더 큰 값을 기준으로 이동
(2) 복잡도
- 원소의 개수가 n인 최대 힙에서 최대 원소 삭제
→ 자식 노드들과 대소 비교 최대 횟수: 2 X log2n
- 최악 복잡도 O(logn)의 삭제 연산
#삭제 연산의 구현
(1) remove() 메서드
class MaxHeap:
def remove(self):
if len(self.data) > 1:
self.data[1], self.data[-1] = self.data[-1], self.data[1]
data = self.data.pop(-1)
self.maxHeapify(1)
else:
data = None
return data(2) maxHeapify() 메서드
class MaxHeap:
def maxHeapify(self, i):
left = i * 2
right = i * 2 + 1
greatest = i
if left < len(self.data) and self.data[left] > self.data[greatest]:
greatest = left
if right < len(self.data) and self.data[right] > self.data[greatest]:
greatest = right
if greatest != i:
self.data[i], self.data[greatest] = self.data[greatest], self.data[i]
self.maxHeapify(greatest)
#최대/최소 힙의 응용
(1) 우선 순위 큐
- Enqueue할 때 "느슨한 정력"을 이루고 있도록 함: O(logN)
- Dequeue할 때 최댓값을 순서대로 추출: O(logN)
(2) 힙 정렬 (heap sort)
- 정렬되지 않은 원소들은 아무 순서로나 최대 힙에 삽입 : O(logN)
- 삽입이 끝나면, 힙이 비어지게 될 때까지 하나씩 삭제 : O(logN)
- 원소들이 삭제되는 순서가 원소들의 정렬 순서
- 정렬 알고리즘 복잡도 : O(NlogN)
#힙 정렬(heap sort)의 코드 구현
def heapSort(unsorted):
H = MaxHeap()
for item in unsorted:
H.insert(item)
sorted = []
d = H.remove()
while d:
sorted.append(d)
d = H.remove()
return sorted
'Python > Data Structure & Algorithm in Python' 카테고리의 다른 글
| [Python 자료 구조] 힙 (Heaps) (0) | 2020.09.11 |
|---|---|
| [Python 자료 구조] 이진 탐색 트리 (Binary Search Trees) (0) | 2020.09.11 |
| [Python 자료구조] 이진 트리 (Binary Trees) (2) | 2020.09.10 |
| [Python 자료 구조] 우선순위 큐 (Priority Queues) (0) | 2020.09.10 |
| [Python 자료구조] 환형 큐(Circular Queue) (0) | 2020.09.10 |




댓글