#연산의 정의
-
size() : 현재 트리에 포함되어 있는 노드의 수를 구함
-
depth() : 현재 트리의 깊이(또는 높이;height)를 구함
-
순회(traversal)
#이진 트리의 구현 - size()
# 이진트리의 구현 - 노드(node)
class Node:
def __init__(self, item):
self.data = item
self.left = None
self.right = None
# 이진 트리의 구현 - 트리(tree)
class BinaryTree:
def __init__(self, r):
self.root = r
class Node:
# 이진 트리의 크기 - 재귀함수 이용
def size(self):
l = self.left.size() if self.left else 0 # 왼쪽 서브트리
r = self.right.size() if self.right else 0 # 오른쪽 서브트리
return l + r + 1 # 왼쪽 + 오른쪽 + 자기자신(+1)
class BinaryTree:
# 크기 구하기
def size(self):
if self.root:
return self.root.size()
else:
return 0
#이진 트리의 구현 - depth()
# depth
def depth(self):
l = self.left.depth() if self.left else 0
r = self.right.depth() if self.right else 0
return max(l,r) + 1
#깊이 우선 순회 (depth first traveral)
(1) 중위 순회 (in-order traversal) : Left subtree → 자기 자신 → Right subtree

# 중위 순회
def inorder(self):
traversal = []
# 왼쪽 서브트리가 존재한다면
if self.left:
traversal += self.left.inorder()
traversal.append(self.data)
# 오른쪽 서브트리가 있다면
if self.right:
traversal += self.right.inorder()
return traversal
(2) 전위 순회 (pre-order traversal) : 자기 자신 → Left subtree → Right subtree

def preorder(self):
traversal = []
traversal.append(self.data)
if self.left:
traversal += self.left.preorder()
if self.right:
traversal += self.right.preorder()
return traversal
(3) 후위 순회 (post-order traversal): Left subtree → Right subtree → 자기 자신

def postorder(self):
traversal = []
if self.left:
traversal += self.left.postorder()
if self.right:
traversal += self.right.postorder()
traversal.append(self.data)
return traversal
#넓이 우선 순회 (breadth first traversal)
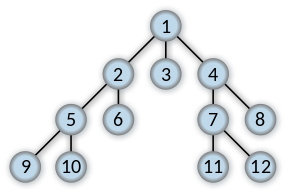
- 수준(Level)이 낮은 노드를 우선으로 방문
- 같은 수준의 노드들 사이에서는 부모 노드의 방문 순서에 따라 방문, 왼쪽 자식 노드를 오른쪽 자식보다 먼저 방문
- 한 노드를 방문했을 때, 나중에 방문할 노드들을 순서대로 기록해 두어야함
→ 선입선출 성질을 가지고 있기 때문에 자료구조는 큐를 사용
def bft(self):
# 빈 리스트 초기화
traversal = []
# 빈 큐 초기화
visitQueue = ArrayQueue()
# 빈 트리가 아니면 루트 노드가 있는 것 -> 큐에 루트 노드를 인큐
if self.root:
visitQueue.enqueue(self.root)
# 큐가 비어있지 않는 동안 반복
while visitQueue.isEmpty()==False:
# 큐에서 꺼내서 node에 저장
node = visitQueue.dequeue()
# 꺼낸 노드를 방문 리스트에 저장
traversal.append(node.data)
# 노드에 왼쪽 자식 노드가 존재하는경우 큐에 저장
if node.left:
visitQueue.enqueue(node.left)
# 노드에 오른쪽 자식 노드가 존재하는 경우 큐에 저장
if node.right:
visitQueue.enqueue(node.right)
return traversal
'Python > Data Structure & Algorithm in Python' 카테고리의 다른 글
| [Python 자료 구조] 힙 (Heaps) (0) | 2020.09.11 |
|---|---|
| [Python 자료 구조] 이진 탐색 트리 (Binary Search Trees) (0) | 2020.09.11 |
| [Python 자료 구조] 우선순위 큐 (Priority Queues) (0) | 2020.09.10 |
| [Python 자료구조] 환형 큐(Circular Queue) (0) | 2020.09.10 |
| [Python 자료구조] 큐 (Queues) (0) | 2020.09.10 |




댓글