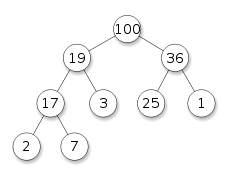
#힙과 이진 탐색 트리 비교
| 구분 | 힙 | 이진 탐색 트리 |
| 원소들은 완전히 크기 순으로 정렬되어 있는가? | X | O |
| 특정 키 값을 가지는 원소를 빠르게 검색할 수 있는가? | X | O |
| 부가의 제약 조건은 어떤 것인가? | 완전 이진 트리이어야 한다. |
#연산의 정의
- init() : 비어 있는 최대 힙을 생성
- insert(item) : 새로운 원소를 삽입
- remove() : 최대 원소(root node)를 반환하고 삭제
#배열을 이용한 이진 트리의 표현

class MaxHeap:
def __init__(self):
self.data = [None]
#최대 힙에 원소 삽입
(1) 방법
- 트리의 마지막 자리에 새로운 원소를 임시로 저장
- 부모 노드의 키 값을 비교하여 위로, 비교하고 위로 이동
(2) 복잡도
- 원소의 개수가 n인 최대 힙에 새로운 원소 삽입
→ 부모 노드와 대소 비교 최대 회수: log2n
→ 최악 복잡도 O(logn)의 삽입 연산
#삽입 연산의 구현 - insert(item) 메서드
class MaxHeap:
def insert(self, item):
# 흰트 - python에서 두 변수의 값 바꾸기
# a = 3, b = 5
# a, b = b, a
self.data.append(item)
index = len(self.data) -1
while index != 1:
numOfParentNode = index//2
print(numOfParentNode)
if self.data[numOfParentNode] < self.data[index]:
self.data[numOfParentNode], self.data[index] = self.data[index], self.data[numOfParentNode]
index = numOfParentNode
else:
break
#최대 힙에서 원소의 삭제
(1) 방법
- 루트 노드의 제거 - 이것이 원소들 중 최대 값
- 트리 마지막 자리 노드를 임시로 루트 노드의 자리에 배치
- 자식 노드들과의 값 비교로 아래로, 비교하여 아래로 이동
→ 자식은 둘이 있을 수 있는데 더 큰 값을 기준으로 이동
(2) 복잡도
- 원소의 개수가 n인 최대 힙에서 최대 원소 삭제
→ 자식 노드들과 대소 비교 최대 횟수: 2 X log2n
- 최악 복잡도 O(logn)의 삭제 연산
#삭제 연산의 구현
(1) remove() 메서드
class MaxHeap:
def remove(self):
if len(self.data) > 1:
self.data[1], self.data[-1] = self.data[-1], self.data[1]
data = self.data.pop(-1)
self.maxHeapify(1)
else:
data = None
return data(2) maxHeapify() 메서드
class MaxHeap:
def maxHeapify(self, i):
left = i * 2
right = i * 2 + 1
greatest = i
if left < len(self.data) and self.data[left] > self.data[greatest]:
greatest = left
if right < len(self.data) and self.data[right] > self.data[greatest]:
greatest = right
if greatest != i:
self.data[i], self.data[greatest] = self.data[greatest], self.data[i]
self.maxHeapify(greatest)
#최대/최소 힙의 응용
(1) 우선 순위 큐
- Enqueue할 때 "느슨한 정력"을 이루고 있도록 함: O(logN)
- Dequeue할 때 최댓값을 순서대로 추출: O(logN)
(2) 힙 정렬 (heap sort)
- 정렬되지 않은 원소들은 아무 순서로나 최대 힙에 삽입 : O(logN)
- 삽입이 끝나면, 힙이 비어지게 될 때까지 하나씩 삭제 : O(logN)
- 원소들이 삭제되는 순서가 원소들의 정렬 순서
- 정렬 알고리즘 복잡도 : O(NlogN)
#힙 정렬(heap sort)의 코드 구현
def heapSort(unsorted):
H = MaxHeap()
for item in unsorted:
H.insert(item)
sorted = []
d = H.remove()
while d:
sorted.append(d)
d = H.remove()
return sorted
'Python > Data Structure & Algorithm in Python' 카테고리의 다른 글
| [Python] 자료구조와 알고리즘 기초 - 재귀 알고리즘, 동적 계획법, 연결리스트, 스택, 큐, 이진트리 (0) | 2020.09.12 |
|---|---|
| [Python 자료 구조] 이진 탐색 트리 (Binary Search Trees) (0) | 2020.09.11 |
| [Python 자료구조] 이진 트리 (Binary Trees) (2) | 2020.09.10 |
| [Python 자료 구조] 우선순위 큐 (Priority Queues) (0) | 2020.09.10 |
| [Python 자료구조] 환형 큐(Circular Queue) (0) | 2020.09.10 |




댓글