*본 포스팅은 중학교 때 수학을 놓아버린 수포자가 기계학습을 이해하기 위해 정리한 것이므로 정확한 정보가 아닐 수 있습니다. 잘못된 정보는 댓글로 알려주시면 감사하겠습니다.
미분은 왜 하며 무엇일까?
미분을 하는 이유는 해당 곡선의 기울기(slope)를 알기 위해서 한다. 미분의 정의는 아래와 같으며 △x대신 'h'를 사용하기도 한다.

'f(x)를 미분하라'는 뜻은 아래 의미를 내포하고 있다.
→ 입력변수 x미세하게 변할 때, 함수 f가 얼마나 변하는지 알 수 있는 식을 구하라.
→ 함수f(x)는 입력 x의 미세한 변화에 얼마나 민감하게 반응하는지 알 수 있느 식을 구하라.

위 그림을 보면 기울기가 (+)이면 녹색이 되고 (-)이면 빨간색이 된다. 기울기가 0이면 검정색이 된다. 기울기는 변화율을 활용하면, y의 변화량(△y)을 x의 변화량(△x)로 나눔으로써 구할 수 있다.
이때의 차분이라는 개념이 등장하는데, 차분은 두 값을 차분은 두값을 뺀 차이를 뜻한다. 즉, x2와 x1 사이의 간격을 의미하며 △x = x2 - x1 와 같이 표현할 수 있다.
위의 차분에서 x1이 x2로 한없이 가까이 가면 이를 미분소라 한다. 예를 들어 x2가 10이라면 x1이 9.99999999...로 x2에 엄청 가까울 때 2와 x1 사이의 간격을 말한다. 미분소는 차분의 극한(limit)으로 생각할 수 있으며, 아래와 같이 표현할 수 있다.
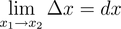
미분을 직관적으로 이해하기

예를 들어 f(x) = x^2일 경우 이를 미분하면 f'(x) =2x이다. 위의 그래프에서 f(3) = 9이며, 이는 입력 x=3에서 출력은 9임을 의미한다. 그리고 f'(x) = 6이며, 입력 x = 3을 미세하게 변화시킬 때 함수의 현재 값의 2배인 6변화를 일으킴을 의미한다.
기계학습에서 '기울기(Gradient)'를 왜 알아야 하는가?
기계학습에서 모든 변수를 편미분을 벡터로 정리한 것을 기울기(Gradient)라고한다. 이는 기계학습에서 손실 함수(loss function, 예측값과 실제값과 차이 정도로 이해하자)를 경사하강법(gradient descent)을 통해 최솟값을 갖는 지점을 찾는다. 여기서 경사하강법(gradient descent)은 기울기를 이용해서 함수의 최솟값이 어디에 있는지 찾는다.
기울기를 통해서 손실함수의 최솟값이 그쪽에 있는지 보는 것이며 최소한의 방향을 나타낸다. (기울기가 0이라고 반드시 그 지점이 최솟값이라고 할 수 없지만 말이다.)

편미분은 무엇인가?
위에서 언급한 편미분은 무엇일까? 편미분은 기본적으로 변수가 하나 이상인 다변수 함수를 대상으로 한다. 변수가 x, y가 있다고 할때 하나의 변수를 미분하고 남은 한 변수를 상수 취급하는 것을 편미분이라고 한다. x 편미분은 아래와 같이 표현할 수 있다.
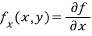
변수가 x,y 두 개인 함수에서 x만 미분할 경우 위와 같이 f뒤에 아래첨자를 적어 준다.
위에 f와 x앞에 있는 문자는 '라운드' 또는 '파샬'이라고 읽는다.
x와 y를 모두 편미분하면 아래와 같다.

편미분을 직관적으로 이해하기
체중 함수가 '체중(야식, 운동)'처럼 야식/운동에 영향을 받는 2변수 함수라고 가정할 경우, 편미분을 이용하면 각 변수의 변화에 따른 체중 변화에 따른 제충 변화량을 구할 수 있다.
'현재 먹는 야식의 양에서 조금씩 변화를 중 경우 체중은 얼마나 변하는가?'는 아래와 같은 식으로 구할 수 있다.

'현재 하고 있는 운동량에 조금 변화를 줄 경우 체중은 얼마나 변하는가?'는 아래와 같은 식으로 구할 수 있다.

'현재 하고 있는 운동량에 조금 변화를 줄 경우 체중은 얼마나 변하는가?'는 아래와 같은 식으로 구할 수 있다.
f(x, y) = 2x+3xy + y^3에서 변수 x에 대하여 편미분하면 아래와 같다.

f(x, y) = 2x+3xy + y^3에서 변수 y에 대하여 편미분하면 아래와 같다.
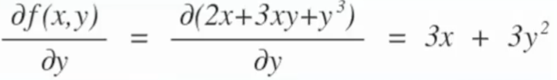
경사하강법(Gradient Descent) 알고리즘과 기울기
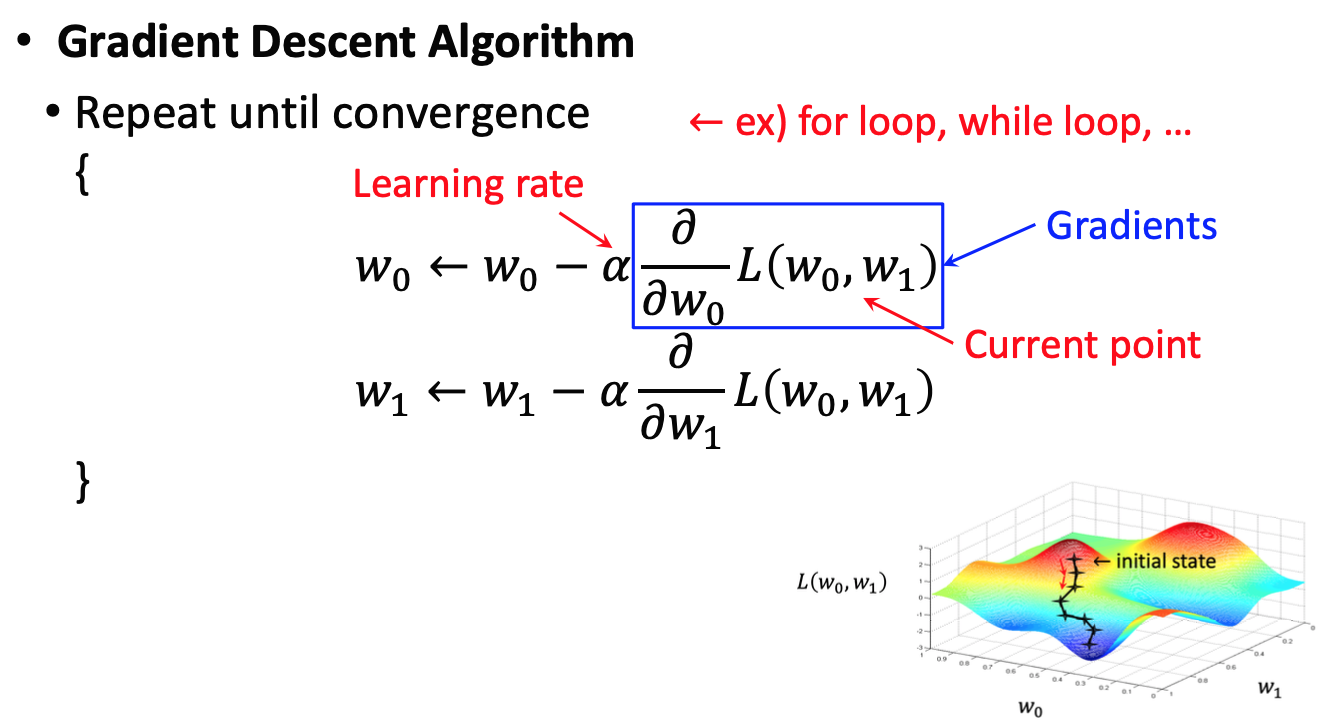
W0와 W1을 찾기 위해서 W0와 W1의 초기값을 설정을 한뒤에 반복 연산(예: for loop, while loop)을 돌린다. 새로운 W를 위해 현재 위치 W에서 Learning rate(알파)와 기울기를 뺀다. 'Gradient의 알파만큼 반대로 움직여라'는 것이며, 이를 경사하강법(Gradient Descent)이라고하 한다.
'Studies & Courses > Machine Learning & Vision' 카테고리의 다른 글
| [ML/DL] 수포자가 이해한 Cross Entropy와 KL-divergence (0) | 2021.01.08 |
|---|---|
| [ML/DL] 수포자가 이해한 2-Layer Neural Net의 vector form (0) | 2021.01.05 |
| [ML/DL] MNIST 손글씨 데이터 인식하기 (0) | 2020.12.31 |
| [ML/DL] 파이썬으로 인공 신경망 만들기 (1) | 2020.12.29 |
| [머신러닝 기초] NumPy Tutorial - Python (0) | 2020.10.24 |




댓글