[ADsP] 추정과 가설검정

1. 데이터 이해 
1-1. 데이터의 이해 
1-2. 데이터의 가치와 미래 
1-3. 가치 창조를 위한 데이터 사이언스와 전략 인사이트 

2. 데이터 분석 기획 
2-1. 데이터 분석 기획의 이해 
2-2. 분석 마스터 플랜 

3. 데이터 분석 
3-1. R 기초와 데이터 마트 

3-2. 통계분석 

  3-2-1. 통계학 개론

  3-2-2. 기초 통계분석

  3-2-3. 다변량 분석

  3-2-4. 시계열 에측

3-3. 정형 데이터 마이닝 

 

 

통계학 개론

통계 분석 개요

확률 및 확률분포

추정과 가설검정

모수 검정

 

 

추정과 가설검정

#추정과 가설검정

통계적 추론
(1) 추정		(2) 가설검정
점추정	구간추정

 - 모수: 통계적 방법론을 통해 알고자하는 대상은 모집단의 확률분포 . 모집단의 특징을 표현하는 값 (예: 평균, 분산, 표준편차, 백분위수 등)

 - 통계적 추론: 모집단에서 추출된 표본을 기반으로 모수들에 대한 통계적 추론을 함. → 추정과 가설검정으로 나뉨

 - 모집단의 평균(모평균)을 추정하기 위한 추정량으로 표본평균이 대표적 (확률표본의 평균값)
 - 모집단의 분산(모분산)을 추정하기 위한 추정량으로 표본분산이 대표적 

 

(1) 점추정: 가장 참값이라고 여겨지는 하나의 모수의 값을 택하는 것. 모수가 특정한 값일 것 이라고 추정하는 것.

(2) 구간추정
 - 모수가 특정한 구간에 있을 것이라는 개념으로 신뢰구간을 추정하는 방법

 - 신뢰수준: 90%, 95%, 99%의 확률을 이용하는 경우가 많다.

 - 신뢰수준 95%: 한 개의 모집단에서 동일한 자료의 개수의 확률표본을 무한히 많이 추출하여 각 확률표본마다 신뢰구간을 구하면, 이 무한히 많은 신뢰구간 중 95%의 신뢰구간이 미지의 모수를 포함한다는 의미.

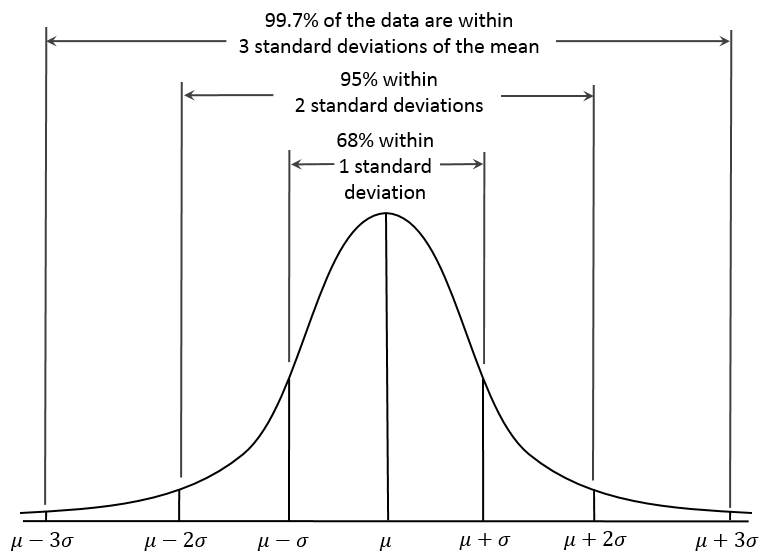
 - 모집단의 획률분포를 정규분포라 가정할 때, 95% 신뢰수준 하에서 모평균 μ 의 신뢰구간

(A visual representation of the Empirical (68-95-99.7) Rule based on the normal distribution, wikipedia)

#가설검정

 - 모집단에 대한 귀무가설(H0)과 대립가설(H1)을 설정한 뒤, 표본관찰 또는 실험을 통해 하나를 선택하는 과정

 - 귀무가설이 옳다는 전제하에서 관측된 검정통계량의 값보다 더 대립가설을 지지하는 값이 나타날 확률을 구하여 가설의 채택여부 결정

 - 귀무가설(H0) : 대립가설과 반대의 증거를 찾기 위해 정한 가설

 - 대립가설(H1) : 증명하고 싶은 가설

 

#p-value

 - 귀무가설이 옳다는 가정하에 얻은 통계량이 귀무가설을 얼마나 지지하는 지를 나타낸 확률

 - p-값이 작을수록 귀무가설을 기각할 가능성이 높아진다.

 - p-값이 유의수준(α)보다 작으면 귀무가설을 기각한다.

 

 

#가설검정의 오류

- 제1종 오류와 제2종 오류는 상충관계가 있음

- 제1종 오류의 확률을 0.1, 0.05, 0.01 등으로 고정시킨 뒤, 제2종 오류가 최소가 되도록 기각역을 설정한다.

- 기각역: 귀무가설을 기각하는 통계량의 영역

정확한 사실\가설검정 결과	귀무가설(H0)이 사실이라고 판정	귀무가설(H0)이 사실이 아니라고 판정
귀무가설(H0)이 사실임	옳은 결정	제 1종 오류(α)
귀무가설(H0)이 사실이 아님	제2종 오류(β)	옳은 결정

 

 

(참고 사이트)

https://logoflife.tistory.com/26

https://m.blog.naver.com/PostView.nhn?blogId=jdhpuppy&logNo=221345226370&proxyReferer=https%3A%2F%2Fwww.google.com%2F