[ADsP] 확률 및 확률분포

1. 데이터 이해 
1-1. 데이터의 이해 
1-2. 데이터의 가치와 미래 
1-3. 가치 창조를 위한 데이터 사이언스와 전략 인사이트 

2. 데이터 분석 기획 
2-1. 데이터 분석 기획의 이해 
2-2. 분석 마스터 플랜 

3. 데이터 분석 
3-1. R 기초와 데이터 마트 

3-2. 통계분석 

  3-2-1. 통계학 개론

  3-2-2. 기초 통계분석

  3-2-3. 다변량 분석

  3-2-4. 시계열 에측

3-3. 정형 데이터 마이닝 

 

 

통계학 개론

통계 분석 개요

확률 및 확률분포

추정과 가설검정

모수 검정

 

 

확률 및 확률분포

#확률의 정의
 - 특정 사건이 일어날 가능성의 척도

 (1) 모든 사건 E의 확률값은 0과 1사이에 있다. 0 <= P(E) <= 1
 (2) 전체 집합 Ω의 확률은 1이다. 즉, P(Ω) = 1
 (3) 서로 배반인 사건들 E1, E2...의 합집합의 확률은 각 사건들의 확률의 합이다. (배반사건 = 교집합이 공집합인 사건)
**표본공간 : 통계적 실험을 실시할 때 나타날 수 있는 모든 결과들의 집합
** 사건 : 표본공간의 부분집합
**근원 사건 : 오직 한 개의 원소로만 이루어진 사건을 근원사건
**표본공간이 유한 개의 원소로 구성이 되어 있고 근원사건들이 일어날 가능성이 모두 같다면, 사건 E의 확률은 " P(E) = n(E)/ n(Ω) " 즉, 사건 수 /  표본공간의 수 이다.

 

 

#조건부 확률과 독립사건
 - 조건부 확률 P(B|A) = P(A n B) / P(A) - P(A)>0 일 때만 정의된다.
 - P(A n B)=P(A)P(B)이면 , 두 사건이 독립이라는 의미.

 - P(B|A)=P(B): 사건 B의 확률은 사건 A가 일어났는 지 여부와 무관하다.

 

 

#확률변수와 확률분포
 - 특정사건이 일어날 확률은 그 변수가 특정값을 가질 확률로 표현할 수 있다.
 - 확률 변수 : 특정값이 나타날 가능성이 확률적으로 주어지는 변수 , 정의역(x값)이 표본 공간, 치역이 실수값

(Image by Julie Bang © Investopedia 2020)

 

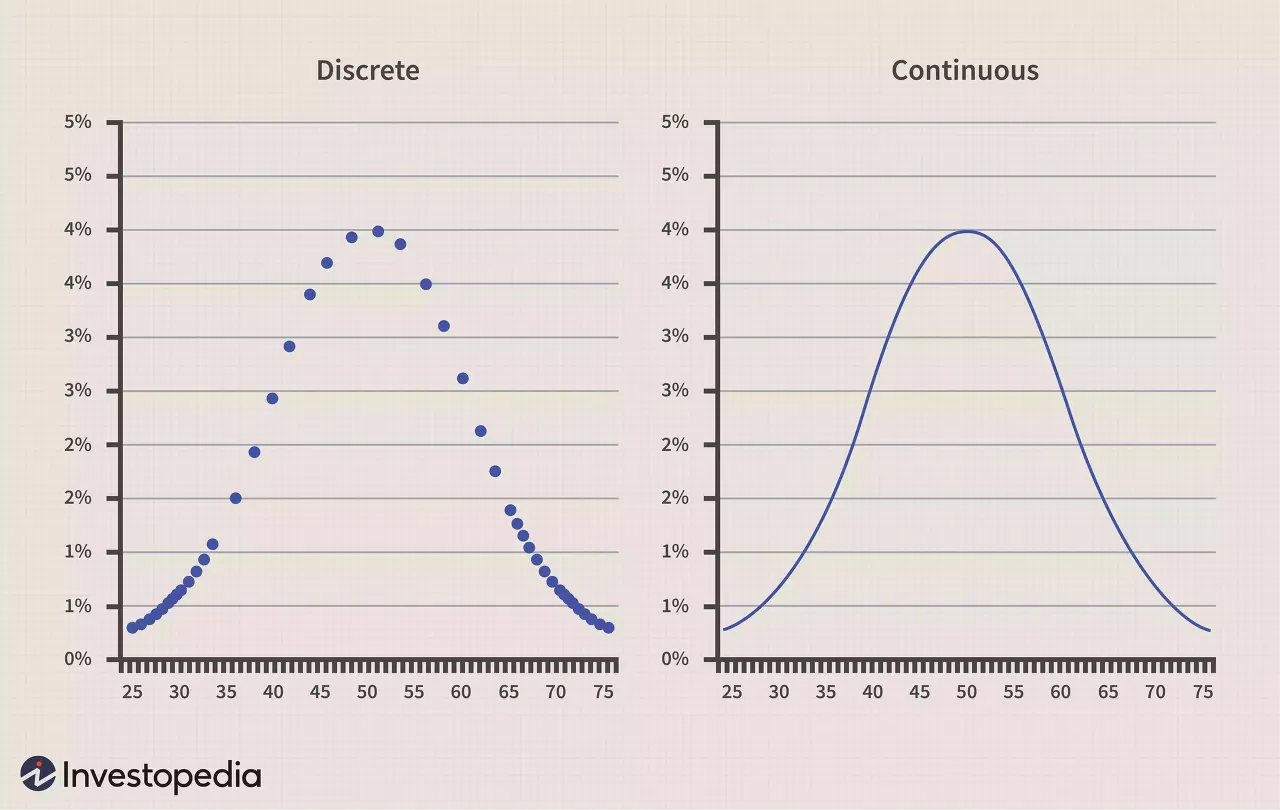
#이산형 확률 변수

 - 사건의 확률이 "점" , 확률이 0보다 큰 값을 갖는 점들로 표현 가능

 - 각 이산점에 있어서 확률의 크기를 표현하는 함수 → 확률 질량 함수

  (1) 베르누이 확률분포: 결과 2개

  (2) 이항분포

  (3) 기하분포: 베르누이 시행 n번 반복 시, k번 성공할 확률

  (4) 포아송분포: 시간, 공간 내에서 발생하는 사건의 횟수에 대한 확률분포

  (5) 다항분포: 이항분포 확장. 3가지 이상의 결과를 가지는 반복 시행에서 발생하는 확률분포

 

 

#연속형 확률 변수

  - 어떤 0보다 큰 값을 갖는 함수의 면적으로 표현
  - 한 점에서의 확률은 0, 구간에서의 확률값 → 확률률밀도함수

  (1) 균일분포(일양분포)

  (2) 정규분포

  (3) 지수분포

  (4) t-분포: 두 집단의 평균이 동일한 지 확인하기 위해 검정통계량으로 활용

  (5) 카이제곱분포: 모평균, 모분산이 알려지지 않는 모집단의 모분산 가설 검정과 동질성 검정 사용

  (6) F-분포: 두 집단 간 분산의 동일성 검정에 사용

#확률변수의 기댓값과 분산
 - 이상형 확률변수의 기댓값은 각 점에서의 확률값의 합

 - 연속형 확률변수의 기댓값은 해당 구간에서의 면적(적분)

 

 

#백분위수

 - 제 q백분위수 Xq 는 P(X<=Xq)=q/100이며, q는 0과 100사이의 값이다.

 

 

(참고 사이트)

https://m.blog.naver.com/jdhpuppy/221345226370

https://m.blog.naver.com/PostView.nhn?blogId=nknn2004&logNo=221824587685&proxyReferer=https:%2F%2Fwww.google.com%2F