1. 데이터 이해
1-1. 데이터의 이해
1-2. 데이터의 가치와 미래
1-3. 가치 창조를 위한 데이터 사이언스와 전략 인사이트
2. 데이터 분석 기획
2-1. 데이터 분석 기획의 이해
2-2. 분석 마스터 플랜
3. 데이터 분석
3-1. R 기초와 데이터 마트
3-2. 통계분석
3-3. 정형 데이터 마이닝
3-3-1. 데이터 마이닝 개요
3-3-2. 분류 분석
3-3-3. 군집 분석
3-3-4. 연관 분석
계층적 군집
#계층적 군집 정의 및 특징
- 가장 유사한 개체를 묶어 나가는 과정을 반복하여 원하는 개수의 군집을 형성하는 방법
(n개의 군집으로 시작해 점차 군집의 개수를 줄어나가는 방법)
- 군집을 형성하는 매 단계에서 지역적 최적화를 수행해 나가는 방법 (전역적인 최적해라고 볼 수 없음)
- 단일, 완전, 평균, 중심결합기준, 와드
- 계층적 군집의 결과는 덴드로그램의 형태로 표현
(* 덴드로그램을 통해 항목간의 거리, 군집간의 거리를 알 수 있고, 항목간 유사정도를 파악하여 견고성을 해석할 수 있다.)
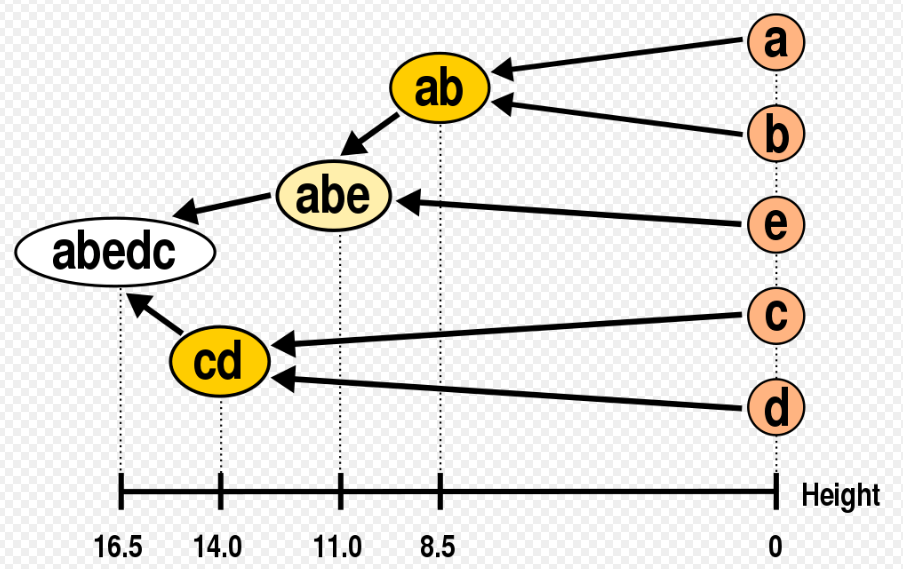
#계층적 군집 방법
1) 병합적(응집형) 방법: Bottom-up
- 작은 군집에서 출발하여 거리가 가까운 순으로 병합해 나가는 방법
(하나의 군집이 남을 때 까지 순차적으로 군집들을 병합)
- R에서 agnes(), mclust() 함수를 이용한다.
2) 분할적(분리형) 방법: Top-down
- 큰 군집에서 출발하여 군집을 분리해 나가는 방법
(하나의 군집에서 n개 군집으로 분리)
- R에서 diana(), mona() 함수를 이용한다.
#군집 간 거리 측정 방법 (연결법)
1) 최단연결법(단일연결법)
- 각 군집에서 관측값을 뽑았을 때 나타날 수 있는 거리의 최소값을 군집간 거리로 한다.
- 사슬 모양으로 생길 수 있음
- 고립된 군집을 찾는데 중점을 둔 방법
2) 최장연결법(완전연결법)
- 각 군집에서 관측값을 뽑았을 때 나타날 수 있는 거리의 최대값을 군집간 거리로 한다.
- 군집들의 내부 응집성에 중점을 둔 방법
3) 중심연결법
- 두 군집의 중심간 거리를 군집간 거리로 한다.
- 군집이 결합될 때, 새로운 군집의 평균은 가중평균을 통해 구해진다.
4) 평균연결법
- 모든 항목에 대한 거리 평균을 구하면서 군집화를 수행한다.
- 계산량이 불필요하게 많아질 수 있다.
4) 와드연결법(ward linkage)
- 군집내의 오차제곱합에 기초하여 군집을 수행한다.
- 군집이 병합되면 오차제곱합은 증가하는데, 증가량이 가장 작아지도록 군집을 형성한다.
- 크기가 비슷한 군집끼리 병합하게 되는 경향이 있다.
#유클리드(유클리디안, Euclidean) 거리
- 데이터간 유사성 측정을 위해 사용, 통계적 개념이 내포X, 변수들의 산포정도 감안X


예시)

#맨하탄(Manhattan) 거리
- 유클리드와 함께 가장 많이 쓰는 거리, 건물간 최단거리 계산 ★
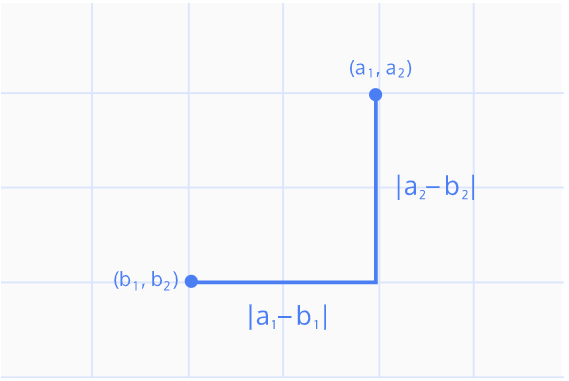

예시)
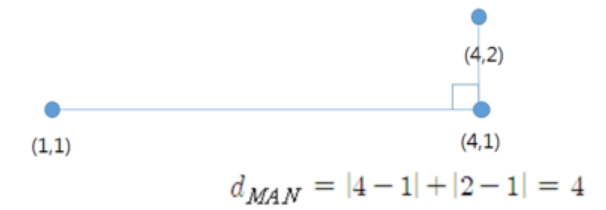
#그 밖의 거리
- 표준화 (Statistical) 거리: 해당 변수의 표준편차로 척도 변환 후 유클리디안 거리를 계산

- 마할라노비스 거리: 통계적 개념이 포함된 거리, 변수들의 산포를 고려하여 표준화한 거리

- 민코우스키(Minkowski) 거리

- 체비셰프 거리 (체스보드 거리, 최고 거리)

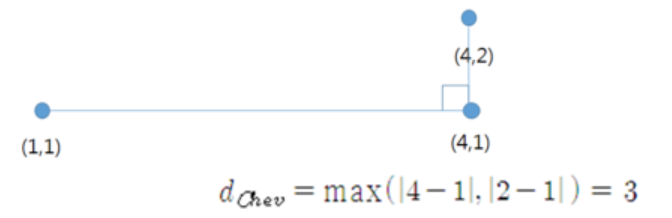
- 캔버라 거리

#군집 간 거리 (연속형, 범주형 변수)
1) 연속형 변수: 유클리디안 거리, 표준화 거리, 마할노비스거리, 체비셰프 거리, 맨하탄 거리, 캔버라 거리, 민코우스키 거리
2) 범주형 변수: 카드 거리, 자카드 계수, 코사인 거리, 코사인 유사도
#군집 간 거리 (수학적, 통계적 거리)
1) 수학적 거리: 유클리드 거리, 맨하튼 거리, 민코우스키 거리
2) 통계적 거리: 표준화 거리, 마할라노비스 거리
(참고 사이트)
https://blog.naver.com/wjddudwo209/80208217440
'Certificates > ADsP' 카테고리의 다른 글
| [ADsP] 분류 분석 - 로지스틱 회귀모형 (0) | 2020.08.06 |
|---|---|
| [ADsP] 군집 분석 - SOM (Self-Organizing Maps, 자기조직화지도) (0) | 2020.08.03 |
| [ADsP] 군집 분석 - 혼합 분포 군집 (EM 알고리즘) (0) | 2020.08.03 |
| [ADsP] 군집 분석 - 비계층적 군집 (K-평균 군집 분석) (0) | 2020.08.03 |
| [ADsP] 의사결정나무 (0) | 2020.08.01 |




댓글