점근표기법(asymptotic notation)
O (빅-오)
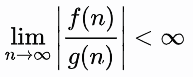
- 점근적 상한에 대한 표기법.
- O(g(n))O(g(n))은 g(n)g(n)의 증가율보다 작거나 같은 함수들의 집합이다.
예를 들어 O(n^2)에는 O(1),O(n),O(nlogn)O(1),O(n),O(nlogn) 등이 포함된다.
- 주어진 알고리즘의 증가율보다 크거나 같은 최소의 증가율을 찾는 것이 목적.
#Big O 표기법 이해하기
- f(x) ≤ c*g(x)을 증명할 수 있으면 f(n) = O(g(n))는 참이다.
- 예시
- f(x) = 2x^2+3, g(x) = x^2 일때, f(x) = O(g(x))는 참인가?
- f(x) = O(g(x)) is true when c=3 x≥2
- f(x) = 2x^2+3, g(x) = x^2 일때, f(x) = O(g(x))는 참인가?
#O(1),O(n),O(logn)O(n^2),O(n^3) 비교

Ω (빅-오메가)

- 점근적 하한에 대한 표기법.
- 주어진 알고리즘의 증가율보다 작거나 같은 최대의 증가율을 찾는 것이 목적.
- n 이 충분히 클 때, 주어진 함수 f(n)의 수행시간은 최상의 경우에도 g(n)과 같거나 더 느리게 실행된다.
#Big Ω 표기법 이해하기
- f(x) > c*g(x)을 증명할 수 있으면 f(n) = Ω(g(n))는 참이다.
- 예시
- f(x) = 2x^2+3, g(x) = x^2 일때, f(n) = Ω(g(n))이 참일 수 있는 C를 찾을 수 있다면 오메가 표기법을 사용할 수 있다.
- f(x) = O(g(x)) is true when c=1
- f(x) = 2x^2+3, g(x) = x^2 일때, f(n) = Ω(g(n))이 참일 수 있는 C를 찾을 수 있다면 오메가 표기법을 사용할 수 있다.
Θ(빅-세타)

- 이 표기법은 주어진 함수(알고리즘)의 상한과 하한이 같은지 아닌지를 결정한다.
- 세타(Θ) 표기법은 항상 상한(O)과 하한(Ω) 사이에 존재한다.
- 상한과 하한이 같다면, 세타 표기법도 같은 증가율을 갖는다.
- n 이 충분히 클 때, 주어진 함수 f(n)은 g(n)의 수행시간 범위 내에 존재한다. (a**(n)과 b**(n) 사이에 있다)
#Big Θ 표기법 이해하기
- f(x) = Θ(g(n))
- 조건: f(x) = O(g(x))과 f(n) = Ω(g(n))이 참이어야 한다.
연습문제
f(n) = logn^2, g(n) = logn + 3
- f(n) = O(g(n)) = ?
- f(n) ≤ c * g(n)
- logn^2 ≤ c * (logn+3)
- 2logn ≤ c * (logn+3)
- c = 2일 때 참이다.
- f(n) = Ω(g(n))
- f(x) > c*g(x)
- 2logn > c*(logn + 3)
- 2logn > (1/10)*(logn + 3)
- 2logn > (1/10)logn + 0.3
- c=1/10, n ≥ 2일 때 참이다.
- f(x) = Θ(g(n))
- 1번과 2번이 참이기 때문에 참이다.
'C, C++ > Data Structure & Algorithm in C' 카테고리의 다른 글
| [자료구조] 합병정렬(Merge Sort) - C언어 (2) | 2020.10.04 |
|---|

댓글